Äquipotentialfläche: Unterschied zwischen den Versionen
- Seiten mit Skriptfehlern
- Elektrostatik
- Erdmessung
imported>Micham6 K (Änderungen von 31.150.39.78 (Diskussion) auf die letzte Version von S.arrhenius zurückgesetzt) |
imported>Nabloodel K (Link auf el. Potential statt auf Unterabschnitt bei Elektrostatik) |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:Aequipotentialflaechen.webm|miniatur|Äquipotentialflächen (rot) für zwei punktförmig konzentrierte Ladungen gleichen Vorzeichens in 3D]] | [[Datei:Aequipotentialflaechen.webm|miniatur|Äquipotentialflächen (rot) für zwei punktförmig konzentrierte Ladungen gleichen Vorzeichens in 3D]] | ||
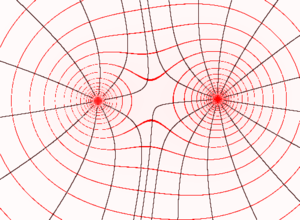
[[Datei:Feldlinien und Äquipotentiallinien.png|miniatur|Äquipotentiallinien (rot) und Feldlinien (schwarz) für zwei punktförmig konzentrierte Ladungen gleichen Vorzeichens]] | [[Datei:Feldlinien und Äquipotentiallinien.png|miniatur|Äquipotentiallinien (rot) und Feldlinien (schwarz) für zwei punktförmig konzentrierte Ladungen gleichen Vorzeichens]] | ||
Eine '''Äquipotentialfläche''', auch '''Äquipotenzialfläche''' oder '''Potenzialfläche''', ist die [[Menge (Mathematik)|Menge]] aller [[Punkt (Geometrie)|Punkte]] gleichen ([[Lateinische Sprache|lateinisch]]: aequalis) [[Potential (Physik)|Potentials]], das heißt gleicher [[Potenzielle Energie|potentieller Energie]] eines Probekörpers in einem [[Potentialfeld]]. Diese Fläche steht | Eine '''Äquipotentialfläche''', auch '''Äquipotenzialfläche''' oder '''Potenzialfläche''', ist die [[Menge (Mathematik)|Menge]] aller [[Punkt (Geometrie)|Punkte]] gleichen ([[Lateinische Sprache|lateinisch]]: aequalis) [[Potential (Physik)|Potentials]], das heißt gleicher [[Potenzielle Energie|potentieller Energie]] eines Probekörpers in einem [[Potentialfeld]]. Diese Fläche steht senkrecht zu den [[Feldlinie]]n und ist ein Spezialfall von [[Isofläche]]n. | ||
Der Verlauf des Potentialfeldes in 2D wird häufig mit Hilfe von Äquipotential-[[Isolinien]] dargestellt. | Der Verlauf des Potentialfeldes in 2D wird häufig mit Hilfe von Äquipotential-[[Isolinien]] dargestellt. | ||
== Elektrisches Potential == | == Elektrisches Potential == | ||
Hier ist sie eine Fläche, deren Punkte alle das gleiche [[ | Hier ist sie eine Fläche, deren Punkte alle das gleiche [[Elektrisches Potential|elektrische Potential]] aufweisen. Somit ist die [[elektrische Spannung|Spannung]] ''U'' zwischen zwei Punkten einer Äquipotentialfläche null. Die zu verrichtende elektrische Arbeit, um einen [[Ladungsträger (Physik)|Ladungsträger]] von einem Punkt der Äquipotentialfläche zu einem anderen Punkt derselben Äquipotentialfläche zu bewegen, ist ebenfalls null. | ||
Ideale [[Leiter (Physik)|Leiter]] sind bei statischen Feldern exakt (bei hinreichend tiefen Frequenzen: fast) Äquipotentialflächen, da jede Potentialdifferenz aufgrund der unendlich hohen [[Elektrische Leitfähigkeit|Leitfähigkeit]] sehr schnell ausgeglichen würde. Bei Metallen (sehr hohe, aber endliche Leitfähigkeit) sind die elektrischen Ladungen ebenfalls frei beweglich. Nur wenn sie keiner Kraft, d. h. keiner [[Elektrische Feldstärke|Feldstärke]], ausgesetzt sind, befinden sie sich im Gleichgewicht. Einem auftretenden Feld folgen sie sehr schnell, bis das Feld kompensiert ist. Daraus ergibt sich, dass (abgesehen von solchen meist kurzzeitigen Ungleichgewichtszuständen) das Potential überall den gleichen Wert besitzt (im Innern und auf der Oberfläche eines Leiters). Für eine ausführliche Diskussion siehe [[Faradayscher_K%C3%A4fig#Erkl.C3.A4rung|Faradayscher Käfig]]. | Ideale [[Leiter (Physik)|Leiter]] sind bei statischen Feldern exakt (bei hinreichend tiefen Frequenzen: fast) Äquipotentialflächen, da jede Potentialdifferenz aufgrund der unendlich hohen [[Elektrische Leitfähigkeit|Leitfähigkeit]] sehr schnell ausgeglichen würde. Bei Metallen (sehr hohe, aber endliche Leitfähigkeit) sind die elektrischen Ladungen ebenfalls frei beweglich. Nur wenn sie keiner Kraft, d. h. keiner [[Elektrische Feldstärke|Feldstärke]], ausgesetzt sind, befinden sie sich im Gleichgewicht. Einem auftretenden Feld folgen sie sehr schnell, bis das Feld kompensiert ist. Daraus ergibt sich, dass (abgesehen von solchen meist kurzzeitigen Ungleichgewichtszuständen) das Potential überall den gleichen Wert besitzt (im Innern und auf der Oberfläche eines Leiters). Für eine ausführliche Diskussion siehe [[Faradayscher_K%C3%A4fig#Erkl.C3.A4rung|Faradayscher Käfig]]. | ||
== Schwerepotential == | == Schwerepotential == | ||
[[Datei: | [[Datei:Gravity anomalies on Earth.jpg|thumb|upright=1.7|Abweichungen vom durchschnittlichen Erdschwerefeld (stark überhöht)]] | ||
Hier ist die Äquipotentialfläche (Niveaufläche, auf der Erde auch Geopotentialfläche) eine Fläche, deren Punkte alle dasselbe (effektive) [[Schwerepotential]] besitzen und dessen [[Gradient (Mathematik)|Gradient]] (räumliche Änderung) man als [[Schwerebeschleunigung]] bezeichnet | Hier ist die Äquipotentialfläche ([[Niveaufläche]], auf der Erde auch Geopotentialfläche) eine Fläche, deren Punkte alle dasselbe (effektive) [[Schwerepotential]] besitzen und dessen [[Gradient (Mathematik)|Gradient]] (räumliche Änderung) man als [[Schwerebeschleunigung]] bezeichnet. | ||
Bei einem rotierenden [[Himmelskörper]] verlaufen die Äquipotentialflächen der Schwere deshalb meist ''nicht'' parallel zur Oberfläche: An den [[Pol (Geographie)|Polen]] des Himmelskörpers etwa ist die effektive Schwerebeschleunigung größer als an seinem [[Äquator]], weshalb die Äquipotentialflächen am Äquator höher liegen als bei einem Punkt am Pol. Aber auch [[Dichte]]<nowiki/>unterschiede im Inneren des Himmelskörpers führen zu Deformationen seines Schwerefeldes. | |||
Analog wird der Begriff in der Meteorologie verwendet, dort bezieht sich der Ausdruck auf die Niveauflächen gleichen Drucks der Atmosphäre, die ebenfalls dem Schwerefeld unterliegt. Für die Praxis hat man [[Hauptdruckfläche]]n definiert (1000, 500, 200 hPa | Das [[Geoid]] ist die Äquipotentialfläche des [[Schwerefeld]]s der Erde auf dem Niveau des mittleren [[Meeresspiegel]]s, also aller Punkte, die dasselbe [[Geopotential]] besitzen, zusammengesetzt aus dem [[Gravitationspotential]] sowie dem [[Zentrifugalkraft|Zentrifugal]]<nowiki/>potential an dem betreffenden Ort. [[Orthometrische Höhe]]n verwenden diese Geopotentialflächen zur Höhendefinition. | ||
Analog wird der Begriff in der [[Meteorologie]] verwendet, dort bezieht sich der Ausdruck auf die Niveauflächen gleichen Drucks der [[Atmosphäre]], die ebenfalls dem Schwerefeld unterliegt. Für die Praxis hat man [[Hauptdruckfläche]]n definiert (1000, 500, 200 [[hPa]] und andere). | |||
== Oberflächenspannung == | == Oberflächenspannung == | ||
Aktuelle Version vom 20. November 2020, 09:41 Uhr
Eine Äquipotentialfläche, auch Äquipotenzialfläche oder Potenzialfläche, ist die Menge aller Punkte gleichen (lateinisch: aequalis) Potentials, das heißt gleicher potentieller Energie eines Probekörpers in einem Potentialfeld. Diese Fläche steht senkrecht zu den Feldlinien und ist ein Spezialfall von Isoflächen.
Der Verlauf des Potentialfeldes in 2D wird häufig mit Hilfe von Äquipotential-Isolinien dargestellt.
Elektrisches Potential
Hier ist sie eine Fläche, deren Punkte alle das gleiche elektrische Potential aufweisen. Somit ist die Spannung U zwischen zwei Punkten einer Äquipotentialfläche null. Die zu verrichtende elektrische Arbeit, um einen Ladungsträger von einem Punkt der Äquipotentialfläche zu einem anderen Punkt derselben Äquipotentialfläche zu bewegen, ist ebenfalls null.
Ideale Leiter sind bei statischen Feldern exakt (bei hinreichend tiefen Frequenzen: fast) Äquipotentialflächen, da jede Potentialdifferenz aufgrund der unendlich hohen Leitfähigkeit sehr schnell ausgeglichen würde. Bei Metallen (sehr hohe, aber endliche Leitfähigkeit) sind die elektrischen Ladungen ebenfalls frei beweglich. Nur wenn sie keiner Kraft, d. h. keiner Feldstärke, ausgesetzt sind, befinden sie sich im Gleichgewicht. Einem auftretenden Feld folgen sie sehr schnell, bis das Feld kompensiert ist. Daraus ergibt sich, dass (abgesehen von solchen meist kurzzeitigen Ungleichgewichtszuständen) das Potential überall den gleichen Wert besitzt (im Innern und auf der Oberfläche eines Leiters). Für eine ausführliche Diskussion siehe Faradayscher Käfig.
Schwerepotential
Hier ist die Äquipotentialfläche (Niveaufläche, auf der Erde auch Geopotentialfläche) eine Fläche, deren Punkte alle dasselbe (effektive) Schwerepotential besitzen und dessen Gradient (räumliche Änderung) man als Schwerebeschleunigung bezeichnet.
Bei einem rotierenden Himmelskörper verlaufen die Äquipotentialflächen der Schwere deshalb meist nicht parallel zur Oberfläche: An den Polen des Himmelskörpers etwa ist die effektive Schwerebeschleunigung größer als an seinem Äquator, weshalb die Äquipotentialflächen am Äquator höher liegen als bei einem Punkt am Pol. Aber auch Dichteunterschiede im Inneren des Himmelskörpers führen zu Deformationen seines Schwerefeldes.
Das Geoid ist die Äquipotentialfläche des Schwerefelds der Erde auf dem Niveau des mittleren Meeresspiegels, also aller Punkte, die dasselbe Geopotential besitzen, zusammengesetzt aus dem Gravitationspotential sowie dem Zentrifugalpotential an dem betreffenden Ort. Orthometrische Höhen verwenden diese Geopotentialflächen zur Höhendefinition.
Analog wird der Begriff in der Meteorologie verwendet, dort bezieht sich der Ausdruck auf die Niveauflächen gleichen Drucks der Atmosphäre, die ebenfalls dem Schwerefeld unterliegt. Für die Praxis hat man Hauptdruckflächen definiert (1000, 500, 200 hPa und andere).
Oberflächenspannung
Flüssigkeiten bilden aufgrund der Oberflächenspannung Äquipotentialflächen (unter Schwerelosigkeit ideale).