Mischungswärme: Unterschied zwischen den Versionen
Kategorien
- Seiten mit Skriptfehlern
- Thermodynamik
imported>Karl Hilpolt (→Beispiele: Angaben für Chloroform/Ethanol waren für T=35 °C statt für 25 °C plus referenz) |
imported>Vfb1893 (BKL Parameter aufgelöst) |
||
| Zeile 3: | Zeile 3: | ||
* Wird die Mischungswärme von den gemischten Stoffen an die Umgebung abgegeben <math>\left( h^E < 0 \right)</math>, so handelt es sich um einen [[exotherm]]en Verlauf | * Wird die Mischungswärme von den gemischten Stoffen an die Umgebung abgegeben <math>\left( h^E < 0 \right)</math>, so handelt es sich um einen [[exotherm]]en Verlauf | ||
In diesem Artikel ist mit dem Formelzeichen h<sup>E</sup> die [[molare Größe|molare]] Mischungswärme gemeint, d.h. die Mischungswärme pro [[Stoffmenge]]. | In diesem Artikel ist mit dem Formelzeichen h<sup>E</sup> die [[molare Größe|molare]] Mischungswärme gemeint, d. h. die Mischungswärme pro [[Stoffmenge]]. | ||
== Beispiele == | == Beispiele == | ||
| Zeile 20: | Zeile 20: | ||
== Modellierung == | == Modellierung == | ||
Mischungswärmekurven<ref>Christensen C., Gmehling J., Rassmussen P., Weidlich U., Holderbaum T., "Heats of Mixing Data Collection", DECHEMA Chemistry Data Series Vol. III., [[DECHEMA]], Frankfurt/M., 1984–1991.</ref> [[binär]]er Mischungen bei einer gegebenen Temperatur können mit den Gleichungen nach ''Redlich-Kister'' (RK) <ref>Redlich O., Kister A.T., "Algebraic Representation of Thermodynamic Properties and the Classification of Solutions", Ind.Eng.Chem., 40(2), 345–348, 1948.</ref> und einer ''Summe symmetrischer Funktionen'' (SSF) beschrieben werden. Beide [[Reihenentwicklung]]en basieren auf folgender einfacher Beziehung, die jedoch nur für wenige Systeme ausreichend genau ist: | Mischungswärmekurven<ref>Christensen C., Gmehling J., Rassmussen P., Weidlich U., Holderbaum T., "Heats of Mixing Data Collection", DECHEMA Chemistry Data Series Vol. III., [[DECHEMA]], Frankfurt/M., 1984–1991.</ref> [[binär]]er Mischungen bei einer gegebenen Temperatur können mit den Gleichungen nach ''Redlich-Kister'' (RK)<ref>Redlich O., Kister A.T., "Algebraic Representation of Thermodynamic Properties and the Classification of Solutions", Ind.Eng.Chem., 40(2), 345–348, 1948.</ref> und einer ''Summe symmetrischer Funktionen'' (SSF) beschrieben werden. Beide [[Reihenentwicklung]]en basieren auf folgender einfacher Beziehung, die jedoch nur für wenige Systeme ausreichend genau ist: | ||
:<math>\frac{h^E}{x_1 \cdot x_2} = A</math> | :<math>\frac{h^E}{x_1 \cdot x_2} = A</math> | ||
| Zeile 32: | Zeile 32: | ||
mit | mit | ||
* A<sub>i</sub>: anpassbarer [[Parameter]] | * A<sub>i</sub>: anpassbarer [[Parameter (Mathematik)|Parameter]] | ||
* n = 1..6 (ein bis sechs Parameter). | * n = 1..6 (ein bis sechs Parameter). | ||
| Zeile 42: | Zeile 42: | ||
* m = 1..3 (zwei, vier oder sechs Parameter). | * m = 1..3 (zwei, vier oder sechs Parameter). | ||
==Literatur== | == Literatur == | ||
<references/> | <references/> | ||
==Siehe auch== | == Siehe auch == | ||
* [[gE-Modelle]] | * [[gE-Modelle]] | ||
* [[Lösungsenthalpie]] | * [[Lösungsenthalpie]] | ||
Aktuelle Version vom 19. November 2020, 19:29 Uhr
Die Mischungswärme hE (auch als Mischungsenthalpie oder Exzessenthalpie bezeichnet) ist die Wärme, die beim Mischen reiner chemischer Stoffe auftritt:
- Wird die Mischungswärme von den gemischten Stoffen aus der Umgebung aufgenommen $ \left(h^{E}>0\right) $, so handelt es sich um einen endothermen Verlauf.
- Wird die Mischungswärme von den gemischten Stoffen an die Umgebung abgegeben $ \left(h^{E}<0\right) $, so handelt es sich um einen exothermen Verlauf
In diesem Artikel ist mit dem Formelzeichen hE die molare Mischungswärme gemeint, d. h. die Mischungswärme pro Stoffmenge.
Beispiele
Abhängig vom Mischungspartner kann das Mischen von Chloroform exo- oder endotherm verlaufen (alle Beispielangaben für ca. 25 °C.):
- Das Mischen mit Tetrahydrofuran verläuft stark exotherm (etwa -2800 J/mol).
- Das Mischen mit Ethanol verläuft je nach gewählter Quell-Stoffmenge[1]
- entweder exotherm (20 mol-% Chloroform und 80 mol-% Ethanol: etwa -650 J/mol)
- oder endotherm (20 mol-% Ethanol und 80 mol-% Chloroform: etwa +400 J/mol)
- Das Mischen mit Cyclohexan verläuft endotherm (etwa +700 J/mol).
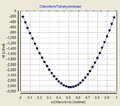
- Mischungsenthalpien bei T = 25 °C
Exotherme Mischungswärme Chloroform /
Tetrahydrofuran
Exo- und endotherme Mischungswärme Chloroform / Ethanol
Endotherme Mischungswärme Chloroform / Cyclohexan
Modellierung
Mischungswärmekurven[2] binärer Mischungen bei einer gegebenen Temperatur können mit den Gleichungen nach Redlich-Kister (RK)[3] und einer Summe symmetrischer Funktionen (SSF) beschrieben werden. Beide Reihenentwicklungen basieren auf folgender einfacher Beziehung, die jedoch nur für wenige Systeme ausreichend genau ist:
- $ {\frac {h^{E}}{x_{1}\cdot x_{2}}}=A $
mit
- $ x_{1} $, $ x_{2} $: Molenbrüche der beiden Komponenten
- $ A $: Konstante.
Redlich-Kister
- $ {\frac {h^{E}}{x_{1}\cdot x_{2}}}=\sum _{i=1}^{n}{A_{i}\left(2x_{1}-1\right)}^{i-1} $
mit
- Ai: anpassbarer Parameter
- n = 1..6 (ein bis sechs Parameter).
Summe symmetrischer Funktionen
- $ {\frac {h^{E}}{x_{1}\cdot x_{2}}}=\sum _{i=1}^{m}{\frac {A_{i}}{\left({\frac {x_{1}}{a_{i}}}+x_{2}a_{i}\right)^{2}}} $
mit
- Ai, ai: anpassbare Parameter
- m = 1..3 (zwei, vier oder sechs Parameter).
Literatur
- ↑ Excess Enthalpy Data. DDBST GmbH, abgerufen am 16. März 2017 (Lua-Fehler in Modul:Multilingual, Zeile 149: attempt to index field 'data' (a nil value)).
- ↑ Christensen C., Gmehling J., Rassmussen P., Weidlich U., Holderbaum T., "Heats of Mixing Data Collection", DECHEMA Chemistry Data Series Vol. III., DECHEMA, Frankfurt/M., 1984–1991.
- ↑ Redlich O., Kister A.T., "Algebraic Representation of Thermodynamic Properties and the Classification of Solutions", Ind.Eng.Chem., 40(2), 345–348, 1948.
Siehe auch
- gE-Modelle
- Lösungsenthalpie
- Aktivitätskoeffizient
- Die Dortmunder Datenbank enthält auch Mischungswärmen.