Bragg-Gleichung: Unterschied zwischen den Versionen
- Seiten mit Skriptfehlern
- Wellenoptik
- Kristallographie
- Spektroskopie
imported>Hadibe K (WP:WPSK ID64; formatiert) |
imported>Acky69 K (zus. Links) |
||
| Zeile 1: | Zeile 1: | ||
Die '''Bragg-Gleichung''', auch '''Bragg-Bedingung''' genannt, wurde 1912 von [[William Lawrence | Die '''Bragg-Gleichung''', auch '''Bragg-Bedingung''' genannt, wurde 1912 von [[William Lawrence Bragg]] entwickelt. Sie beschreibt, wann es zu konstruktiver [[Interferenz (Physik)|Interferenz]] von [[Welle]]n bei [[Streuung (Physik)|Streuung]] an einem dreidimensionalen Gitter kommt. Sie erklärt die Muster, die bei der [[Beugung (Physik)|Beugung]] von [[Röntgenstrahlung|Röntgen-]] oder [[Neutronenstrahlung]] an [[Kristall|kristallinen Festkörpern]] entstehen, aus der [[Periodizität]] von [[Gitterebene]]n. | ||
Das Analogon zur Bragg-Bedingung im [[Reziproker Raum|reziproken Raum]] ist die [[Laue-Bedingung]]. | |||
== Prinzip == | == Prinzip == | ||
| Zeile 23: | Zeile 25: | ||
:<math>{\sin(\theta)}^2=\frac{\lambda^2}{4\, {a_0}^2} (h^2+k^2+l^2)</math> | :<math>{\sin(\theta)}^2=\frac{\lambda^2}{4\, {a_0}^2} (h^2+k^2+l^2)</math> | ||
Für ''n = 1'' sind die Laue-Indizes mit den [[Millersche Indizes|Miller-Indizes]] identisch. Für höhere Ordnungen ''n'' steht ''hkl'' für die [[Laue-Indizes]], die mit der Beugungsordnung ''n'' multiplizierten Miller-Indizes der Gitterebene.<ref>Borchardt-Ott, Kristallographie, Springer 2009, S. 284 f | Für ''n = 1'' sind die Laue-Indizes mit den [[Millersche Indizes|Miller-Indizes]] identisch. Für höhere Ordnungen ''n'' steht ''hkl'' für die [[Laue-Indizes]], die mit der Beugungsordnung ''n'' multiplizierten Miller-Indizes der Gitterebene.<ref>Borchardt-Ott, Kristallographie, Springer 2009, S. 284 f.</ref> | ||
== Physikalischer Hintergrund == | == Physikalischer Hintergrund == | ||
| Zeile 37: | Zeile 39: | ||
[[Datei:Braggs Law.svg|mini|Beugungsgeometrie bei konstruktiver Interferenz (links) und destruktiver Interferenz (rechts)]] | [[Datei:Braggs Law.svg|mini|Beugungsgeometrie bei konstruktiver Interferenz (links) und destruktiver Interferenz (rechts)]] | ||
Die blauen Linien ( | Die blauen Linien in der nebenstehenden Grafik (Schema zur Beugungsgeometrie) entsprechen [[Strahlenoptik|Strahlen]], die auf parallele Gitterebenen treffen und dabei mit dem Lot den Winkel <math>\alpha</math> einschließen. Der [[Komplementärwinkel]] <math>\theta = 90^\circ - \alpha</math> heißt ''Braggwinkel'' oder ''Glanzwinkel''. ''d'' ist der Gitterebenenabstand, die schwarzen Punkte sind Atome auf den Gitterebenen. | ||
Aufgrund der großen Anzahl von Atomen in einem Kristall gibt es für den Fall nicht ausschließlich konstruktiver Interferenz statistisch zu jedem Atom immer ein zweites, das die gebeugte Welle des ersten genau auslöscht, so dass keine Reflexion mehr beobachtet werden kann. Dies ist auch die Situation in [[Amorphes Material|nicht-kristallinem Material]], unabhängig von der Einstrahlrichtung. | Aufgrund der großen Anzahl von Atomen in einem Kristall gibt es für den Fall nicht ausschließlich konstruktiver Interferenz statistisch zu jedem Atom immer ein zweites, das die gebeugte Welle des ersten genau auslöscht, so dass keine Reflexion mehr beobachtet werden kann. Dies ist auch die Situation in [[Amorphes Material|nicht-kristallinem Material]], unabhängig von der Einstrahlrichtung. | ||
| Zeile 55: | Zeile 57: | ||
== Durchführung des Versuchs == | == Durchführung des Versuchs == | ||
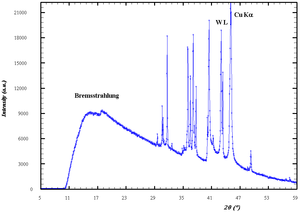
[[Datei:Tube Cu LiF.PNG|mini| | [[Datei:Tube Cu LiF.PNG|mini|Emissionsspektrum einer Kupferanode mit Röntgenstrahlung unterschiedlicher Wellenlänge (bzw. hier als Winkel aufgetragen).]] | ||
Die Drehkristallanordnung ist eine mögliche Durchführung des Versuchs. Da frühere Röntgenapparate sehr schwer und somit nicht drehbar waren, wurde der Röntgenstrahl auf einen drehbaren Kristall gelenkt. Durch Drehung des Kristalls und des Empfängers konnte der Kristall dann unter verschiedenen Winkeln untersucht werden. | Die Drehkristallanordnung ist eine mögliche Durchführung des Versuchs. Da frühere Röntgenapparate sehr schwer und somit nicht drehbar waren, wurde der Röntgenstrahl auf einen drehbaren Kristall gelenkt. Durch Drehung des Kristalls und des Empfängers konnte der Kristall dann unter verschiedenen Winkeln untersucht werden. | ||
| Zeile 65: | Zeile 67: | ||
* Beugungsbilder von Elektronenstrahlen können in [[Elektronenmikroskop]]en hergestellt und beobachtet werden. Auch diese werden grundlegend durch das Bragg-Gesetz beschrieben. | * Beugungsbilder von Elektronenstrahlen können in [[Elektronenmikroskop]]en hergestellt und beobachtet werden. Auch diese werden grundlegend durch das Bragg-Gesetz beschrieben. | ||
* Bragg-Reflexionen treten bei sog. [[Hologramm|Weißlichthologrammen]] auf. Dort sind sie dafür verantwortlich, dass das Bild des Hologramms beim Kippen seine Farbe ändert. | * Bragg-Reflexionen treten bei sog. [[Hologramm|Weißlichthologrammen]] auf. Dort sind sie dafür verantwortlich, dass das Bild des Hologramms beim Kippen seine Farbe ändert. | ||
* Bragg- | * [[Bragg-Spiegel|Bragg-Reflektor]]en werden zur Wellenlängenselektion bei [[Laser]]n oder Röntgenstrahlen eingesetzt (siehe u. a. [[Monochromator]], [[DBR-Laser]], [[DFB-Laser]]). | ||
* [[Akustooptischer Modulator|Akustooptische Modulatoren]] basieren auf dem Prinzip der Bragg-Beugung; Lichtstrahlen werden hierbei an einem wandernden optischen Gitter, hervorgerufen durch longitudinale Schallwellen in Kristallen, gebeugt. | * [[Akustooptischer Modulator|Akustooptische Modulatoren]] basieren auf dem Prinzip der Bragg-Beugung; Lichtstrahlen werden hierbei an einem wandernden optischen Gitter, hervorgerufen durch longitudinale Schallwellen in Kristallen, gebeugt. | ||
== Literatur == | == Literatur == | ||
* [[Dieter Meschede]]: ''Gerthsen Physik.'' 22. Auflage, Springer-Verlag, Berlin/Heidelberg 2004, ISBN 3-540-02622-3. | * [[Dieter Meschede]]: ''Gerthsen Physik.'' 22. Auflage, Springer-Verlag, Berlin/Heidelberg 2004, ISBN 3-540-02622-3. | ||
* [[Rudolf Allmann]]: ''Röntgen-Pulver-Diffraktometrie.'' Verlag Sven von Loga, Köln 1994, ISBN 3-87361-029-9. | * [[Rudolf Allmann (Kristallograph)|Rudolf Allmann]]: ''Röntgen-Pulver-Diffraktometrie.'' Verlag Sven von Loga, Köln 1994, ISBN 3-87361-029-9. | ||
* Werner Massa: ''Kristallstrukturbestimmung.'' 5. Auflage, Teubner-Verlag, Stuttgart/Leipzig/Wiesbaden 2007, ISBN 3-8351-0113-7. | * Werner Massa: ''Kristallstrukturbestimmung.'' 5. Auflage, Teubner-Verlag, Stuttgart/Leipzig/Wiesbaden 2007, ISBN 3-8351-0113-7. | ||
* Anthony R. West: ''Grundlagen der Festkörperchemie.'' Wiley-VCH, Weinheim 2000, ISBN 3-527-28103-7. | * Anthony R. West: ''Grundlagen der Festkörperchemie.'' Wiley-VCH, Weinheim 2000, ISBN 3-527-28103-7. | ||
Aktuelle Version vom 8. Februar 2022, 11:16 Uhr
Die Bragg-Gleichung, auch Bragg-Bedingung genannt, wurde 1912 von William Lawrence Bragg entwickelt. Sie beschreibt, wann es zu konstruktiver Interferenz von Wellen bei Streuung an einem dreidimensionalen Gitter kommt. Sie erklärt die Muster, die bei der Beugung von Röntgen- oder Neutronenstrahlung an kristallinen Festkörpern entstehen, aus der Periodizität von Gitterebenen.
Das Analogon zur Bragg-Bedingung im reziproken Raum ist die Laue-Bedingung.
Prinzip
Trifft Röntgenstrahlung auf einen Kristall, so wird dieser von einem Großteil der Strahlung ungehindert durchdrungen. Es wird allerdings auch beobachtet, dass ein kleiner Teil durch den Kristall abgelenkt wird – ein Phänomen, das man als Röntgenbeugung bezeichnet. Montiert man hinter dem Kristall einen geeigneten Detektor, zum Beispiel eine Fotoplatte, um die abgelenkten Strahlungsanteile sichtbar zu machen, entstehen darauf charakteristische Muster.
Ursache für die Beugung ist die Streuung der Röntgenstrahlung an den einzelnen Atomen des Gitters. Dies kann man auch als eine schwache Reflexion der Röntgenstrahlung an den einzelnen Gitterebenen des Kristalls betrachten, wobei die Strahlung nur in solche Richtungen nennenswert reflektiert wird, in denen die einzelnen Reflexionen sich konstruktiv überlagern. Diese Bedingung beschreibt die Bragg-Gleichung:
- $ n\lambda =2d\,\sin(\theta ) $
Die Bragg-Gleichung verknüpft:
- den Abstand d zwischen parallelen Gitterebenen,
- die Wellenlänge $ \lambda $ der Röntgenstrahlung sowie
- den Winkel $ \theta $ zwischen Röntgenstrahl und Gitterebene, sogenannter Glanz- oder Braggwinkel,
- n ist eine natürliche Zahl, die die Beugungsordnung angibt.
Jede Schar paralleler Gitterebenen hat einen charakteristischen Gitterebenenabstand d und damit, so die Bragg-Gleichung, auch einen charakteristischen Braggwinkel $ \theta $. Für verschiedene Orientierungen, unter denen Strahlung auf den Kristall trifft, erhält man auf dem Detektor hinter dem Kristall fast immer auch verschiedene Bilder, weil sich immer andere Scharen paralleler Gitterebenen (mit anderen Braggwinkeln und mit anderen Orientierungen im Kristall) in Reflexionsstellung zum einfallenden Strahl befinden.
Die Gitterebenen werden üblicherweise mit Laue-Indizes hkl gekennzeichnet, so dass sich für den Abstand zum Beispiel im kubischen System ergibt:
- $ d_{hkl}={\frac {a_{0}}{\sqrt {h^{2}+k^{2}+l^{2}}}} $
mit der Gitterkonstanten $ a_{0} $. Die Bragg-Bedingung lautet damit im kubischen System:
- $ {\sin(\theta )}^{2}={\frac {\lambda ^{2}}{4\,{a_{0}}^{2}}}(h^{2}+k^{2}+l^{2}) $
Für n = 1 sind die Laue-Indizes mit den Miller-Indizes identisch. Für höhere Ordnungen n steht hkl für die Laue-Indizes, die mit der Beugungsordnung n multiplizierten Miller-Indizes der Gitterebene.[1]
Physikalischer Hintergrund
Tatsächlich handelt es sich um ein Beugungsphänomen. Im elektromagnetischen Feld der einfallenden Strahlung werden die Elektronen der Atome zu erzwungenen Schwingungen angeregt und beginnen selbst Strahlung in Form von kugelförmigen Wellen abzustrahlen. Da die Wellen der einzelnen Elektronen sich in erster Näherung zu Wellen der zugehörigen Atome aufsummieren, und weiterhin die Abstände im Kristallgitter und die Wellenlänge der Röntgenstrahlung von ähnlicher Größenordnung sind, treten Interferenzerscheinungen auf.
Ist die Bragg-Gleichung bei gegebener Wellenlänge $ \lambda $ für eine Schar von parallelen Gitterebenen erfüllt, das heißt, trifft die Röntgenstrahlung unter dem richtigen Winkel auf den Kristall, kommt es zu konstruktiver Interferenz der bei der Beugung an den Elektronenhüllen entstehenden Kugelwellen. Makroskopisch entsteht der Eindruck einer Reflexion der Strahlung am Kristall.
Herleitung
Die blauen Linien in der nebenstehenden Grafik (Schema zur Beugungsgeometrie) entsprechen Strahlen, die auf parallele Gitterebenen treffen und dabei mit dem Lot den Winkel $ \alpha $ einschließen. Der Komplementärwinkel $ \theta =90^{\circ }-\alpha $ heißt Braggwinkel oder Glanzwinkel. d ist der Gitterebenenabstand, die schwarzen Punkte sind Atome auf den Gitterebenen.
Aufgrund der großen Anzahl von Atomen in einem Kristall gibt es für den Fall nicht ausschließlich konstruktiver Interferenz statistisch zu jedem Atom immer ein zweites, das die gebeugte Welle des ersten genau auslöscht, so dass keine Reflexion mehr beobachtet werden kann. Dies ist auch die Situation in nicht-kristallinem Material, unabhängig von der Einstrahlrichtung.
- Die Phasenbeziehung bleibt unverändert und es tritt konstruktive Interferenz auf, wenn die in der oberen Darstellung dunkelblau gekennzeichnete Wegdifferenz zwischen oberem und unterem Wellenzug (der Gangunterschied $ 2\delta $) einem ganzzahligen Vielfachen der Wellenlänge $ \lambda $ entspricht:
- $ 2\delta =n\cdot \lambda $
- wobei n auch als Beugungsordnung bezeichnet wird.
- In der oberen Darstellung bilden rote, grüne und lilafarbene Linien zusammen ein rechtwinkliges Dreieck mit der Hypotenuse d. Die Sinusdefinition verhilft zu folgendem Ausdruck:
- $ \delta =d\cdot \sin(\theta ) $
- Wichtig für das Verständnis ist, dass es sich bei den roten Linien nicht um Verlängerungen der oberen hellblauen Linien handelt, sondern um die Senkrechten dazu.
- Setzt man den zweiten Ausdruck in die erste Gleichung ein, erhält man sofort die Bragg-Gleichung (auch Braggsche Interferenz):
- $ n\lambda =2d\,\sin(\theta ) $
Durchführung des Versuchs
Die Drehkristallanordnung ist eine mögliche Durchführung des Versuchs. Da frühere Röntgenapparate sehr schwer und somit nicht drehbar waren, wurde der Röntgenstrahl auf einen drehbaren Kristall gelenkt. Durch Drehung des Kristalls und des Empfängers konnte der Kristall dann unter verschiedenen Winkeln untersucht werden. Eine zweite Möglichkeit stellt das Debye-Scherrer-Verfahren dar, bei dem der Kristall pulverisiert wird, so dass jede „Drehrichtung“ statistisch verteilt gleichzeitig vorhanden ist.
Bedeutung
- Röntgenbeugungsexperimente an Kristallen bieten die Möglichkeit, Einblicke in die innere Struktur von Kristallen zu erlangen (siehe: Kristallstrukturanalyse).
- Gleicherweise ist die Braggreflexion für die Neutronenbeugung bedeutend. Moderierte Neutronen haben vergleichbare Wellenlängen wie Röntgenstrahlen, so dass das gleiche Phänomen am Kristallgitter auftritt.
- Beugungsbilder von Elektronenstrahlen können in Elektronenmikroskopen hergestellt und beobachtet werden. Auch diese werden grundlegend durch das Bragg-Gesetz beschrieben.
- Bragg-Reflexionen treten bei sog. Weißlichthologrammen auf. Dort sind sie dafür verantwortlich, dass das Bild des Hologramms beim Kippen seine Farbe ändert.
- Bragg-Reflektoren werden zur Wellenlängenselektion bei Lasern oder Röntgenstrahlen eingesetzt (siehe u. a. Monochromator, DBR-Laser, DFB-Laser).
- Akustooptische Modulatoren basieren auf dem Prinzip der Bragg-Beugung; Lichtstrahlen werden hierbei an einem wandernden optischen Gitter, hervorgerufen durch longitudinale Schallwellen in Kristallen, gebeugt.
Literatur
- Dieter Meschede: Gerthsen Physik. 22. Auflage, Springer-Verlag, Berlin/Heidelberg 2004, ISBN 3-540-02622-3.
- Rudolf Allmann: Röntgen-Pulver-Diffraktometrie. Verlag Sven von Loga, Köln 1994, ISBN 3-87361-029-9.
- Werner Massa: Kristallstrukturbestimmung. 5. Auflage, Teubner-Verlag, Stuttgart/Leipzig/Wiesbaden 2007, ISBN 3-8351-0113-7.
- Anthony R. West: Grundlagen der Festkörperchemie. Wiley-VCH, Weinheim 2000, ISBN 3-527-28103-7.
Weblinks
Einzelnachweise
- ↑ Borchardt-Ott, Kristallographie, Springer 2009, S. 284 f.