Keimbildung: Unterschied zwischen den Versionen
- Seiten mit Skriptfehlern
- Thermodynamik
- Niederschlag
- Wolke
- Festkörperchemie
- Kristallzüchtung
- Kristallographie
imported>Textkontrolle (→Klassische Keimbildungstheorie: uns, wir?) |
imported>Aka K (→Einzelnachweise: Kategorie hinzugefügt) |
||
| Zeile 1: | Zeile 1: | ||
{{Weiterleitungshinweis|Nukleation|Für die initiale Phase in der | {{Weiterleitungshinweis|Nukleation|Für die initiale Phase in der Biochemie siehe [[Nukleations-Kondensations-Modell]]}} | ||
'''Keimbildung''' oder '''Nukleation''' ist der grundlegende Prozess, bei dem sich an einer '''Keimstelle''' ein '''Nukleationskeim''' bildet, der als "Startkomponente" einen [[Phasenübergang]] erster Ordnung einleitet. | |||
'''Keimbildung''' oder '''Nukleation''' ist der | |||
Beispiele für einen Phasenübergang sind | |||
* die [[Kondensation]] von [[Dampf]] zu Flüssigkeit | |||
* sowie umgekehrt: die [[Blase (Physik)|Blasen]]<nowiki/>bildung beim Übergang von der flüssigen zur gasförmigen [[Phase (Materie)|Phase]] | |||
* der Beginn einer [[Kristallisation]] | |||
** [[Gefrieren]] einer Flüssigkeit | |||
** Abscheidung durch [[Resublimation]] direkt aus der Gasphase | |||
** Bildung von [[Kristall|kristallinen Festkörpern]] aus einer [[übersättigt]]en [[Lösung (Chemie)|Lösung]] | |||
** [[Kristallit]]<nowiki/>bildung bei Abkühlung einer [[Schmelze]] (beispielsweise [[Bainit]]­bildung) | |||
* [[Entmischung (Thermodynamik)|Entmischung]]svorgänge zweier flüssiger Phasen. | |||
* weitere Phasenübergangsformen siehe [[Phasenübergang #Weitere Klassifikationen]]. | |||
Bei stärkerer [[Übersättigung]] oder [[Unterkühlung (Thermodynamik)|Unterkühlung]] kann die Keimbildung spontan erfolgen.<ref>VDI 3491 Blatt 4:2018-03 ''Messen von Partikeln; Herstellungsverfahren für Prüfaerosole; Kondensationsverfahren (Measurement of particles; Methods for generating test aerosols; Condensation methods).'' Beuth Verlag, Berlin, S. 4.</ref> Lokale Dichtefluktuationen (statistische Schwankungen (=[[Fluktuation]]en) des Aufenthaltsortes der Moleküle nach [[Cluster (Physik)|Mikroclusterbildung]] auf molekularer Ebene) führen dabei zu Dichte- und Druckunterschieden (wie sie auch bei der [[Natürliche Konvektion|Thermokonvektion]] auftreten) und so zur Keimbildung. | |||
Auch die allgegenwärtige [[kosmische Strahlung]] erzeugt [[Stoßionisation|stoßionisierte]] Moleküle und bildet so (wie in einer [[Nebelkammer]]) Kondensationskeime für [[Nebel]]- und [[Wolke]]nbildung. | |||
== Allgemeines == | == Allgemeines == | ||
Wesentliches Merkmal der Keimbildung ist, dass die neue, bei den gegebenen Bedingungen [[Gleichgewicht (Systemtheorie)#stabil|thermodynamisch stabile Phase]], zunächst durch Keime aus der alten, [[Metastabilität|metastabilen Phase]] gebildet wird. Unter einem einzelnen Keim versteht man hierbei einen kleinen in der Regel nur wenige Nanometer umfassenden räumlich [[Homogenität|homogenen]] Bereich der neuen Phase innerhalb der alten Phase. | |||
Die Bildung dieser typischerweise nur [[nanometer]]<nowiki/>großen Keime ist zunächst kinetisch gehemmt (bei kinetischer Hemmung ist die [[Kinetik (Chemie)#Reaktionsgeschwindigkeit|Reaktionsgeschwindigkeit]] sehr klein und deswegen eine [[Aktivierungsenergie]] nötig;<ref>Hans Peter Latscha, Helmut Alfons Klein: ''Anorganische Chemie.'' Springer-Verlag, 2013, ISBN 3662057573 S. 243 ({{Google Buch|BuchID=SND1BQAAQBAJ|Seite=243}}).</ref> siehe dazu auch [[Sterische Hinderung]]). [[Flüssigkeit]]en lassen sich [[Unterkühlung (Thermodynamik)|unterkühlen]] und [[Siedeverzug|überhitzen]]. Der Grund für diese Hemmung liegt in der [[Arbeit (Physik)|Arbeit]], die aufgebracht werden muss, um die gekrümmte Oberfläche eines kleinsten Keims (z. B. ein kugelförmiges [[Tropfen|Tröpfchen]]) der neuen Phase zu bilden. Für kleinste Tröpfchen oder [[Kristall]]e ist diese [[Oberflächenspannung|Oberflächenarbeit]] größer als der Energiegewinn aus dem Übergang in die neue, stabile Phase. Die daraus entstehende freie Energiebarriere nennt man '''Keimbildungsbarriere''' und die Arbeit, die aufgebracht werden muss, um diese Barriere zu überwinden, '''Keimbildungsarbeit''' (vgl. unten Thermodynamik). Der Bereich des [[Phasendiagramm]]s, in dem die Keime unterhalb der kritischen Keimgröße bleiben, wird [[Ostwald-Miers-Bereich]] genannt. | |||
Sind jedoch einmal Keime, die größer sind als die kritische Keimgröße, aus thermischen [[Fluktuation]]en gebildet, so wachsen sie schnell zur makroskopischen Phase an. Keimbildung kann damit auch als Prototyp eines aktivierten Prozesses verstanden werden. | |||
Die ''Keimbildungsrate'' beschreibt, wie viele Keime der neuen Phase pro Volumen- und Zeiteinheit gebildet werden. Diese Keimbildungsrate hängt stark exponentiell von der Keimbildungsarbeit ab | Die '''Nukleationsrate''' oder '''Keimbildungsrate''' beschreibt, wie viele Keime der neuen Phase pro Volumen- und Zeiteinheit gebildet werden. Diese Keimbildungsrate hängt stark exponentiell von der Keimbildungsarbeit ab: je höher die Keimbildungsarbeit und damit die Barriere zur Keimbildung, desto niedriger die Rate (vgl. unten Kinetik). | ||
[[Datei:Heating pad in action.ogv|mini|Kristallisation der Flüssigkeit eines [[Wärmekissen]]s nach erfolgter Keimbildung]] | |||
== Auftreten == | |||
Keimbildung ist ein allgegenwärtiger Prozess. Beispielsweise bildet [[Rauheit]] an einer Behälterwandung Keimstellen für ausgasendes [[Kohlenstoffdioxid|CO<sub>2</sub>]]. [[Feinstaub]] und sonstiger [[Schwebstaub]] können Kondensationskeime bei der Bildung von [[Nebel]]- oder [[Niederschlag|Regenwolken]] liefern. In einem [[Wärmekissen]] liefert ein umgeknicktes Metallplättchen die nötigen Kristallisationskeime. | |||
Für die Industrie ist die Kenntnis der Keimbildungskinetik von höchstem Interesse, z. B. um den [[Tropfenschlag]] in [[Gasturbine]]n oder den [[Siedeverzug]] in [[Verdampfer (Verfahrenstechnik)|Verdampfern]] zu verhindern oder um die Bildung des [[Kondensstreifen]]s bei [[Düsenflugzeug]]en zu kontrollieren. Die Nukleation spielt darüber hinaus eine zentrale Rolle in der [[Verfahrenstechnik]] von [[Polymer]]en, [[Legierung]]en sowie manchen [[Keramik]]en, aber auch bei der Kontrolle bzw. Verhinderung der [[Kristallisation]] (z. B. bei [[Halbleiter]]materialien, [[Metallisches Glas|metallischen Gläsern]] oder [[Honig]]). | |||
[[Electrofreezing]] ist ein Verfahren, durch das die [[Kristallisation]] von Wasser und anderen Flüssigkeiten beim [[Gefrieren|Gefrierprozess]] gezielt durch das Anlegen eines [[elektrisches Feld|elektrischen Feldes]] ausgelöst werden kann. Dieses physikalische Phänomen ist seit 1861 bekannt. | |||
[[Datei:Tropfendimensionen.png|mini|Größendimensionen von Regentropfen im Vergleich zu einem Kondensationskeim<ref>[https://www.meteo.physik.uni-muenchen.de/lehre/roger/Einfuehrung_Teil_III/Einfuehrung_Teil_III_Kapital-1.pdf Aerosol und Wolkenphysik], S. 5</ref>]] | |||
=== Kondensationskeime === | |||
Ein '''Kondensationskeim''' oder auch '''Kondensationskern''' erleichtert die Keimbildung und die folgende Kondensation eines [[gas]]­förmigen Stoffes. Ein solcher Keim kann eine Verschmutzung sein, wie ein [[Staub]]-, [[Salze|Salz]]- oder [[Ruß]][[Teilchen#Verwandte Begriffe|partikel]], oder [[Ionisiert|ionisierte]] Gasmoleküle, wie bei der [[Nebelkammer]]. Der Nachweis von Kondensationskernen gelang P. J. Coulier im Jahr 1875.<ref>Carsten Möhlmann: ''[https://www.dguv.de/medien/ifa/de/pub/grl/pdf/2005_071.pdf Staubmesstechnik - damals bis heute].'' In: ''[[Gefahrstoffe – Reinhaltung der Luft|Gefahrstoffe – Reinhalt. Luft]].'' 65, Nr. 5, 2005, {{ISSN|0949-8036}}, S. 191–194. (PDF; 335 kB)</ref> | |||
[[ | ==== Beispiele ==== | ||
* [[Aerosol]]<nowiki/>partikel, die bestimmte chemische und physikalische Eigenschaften besitzen, fungieren in der [[Erdatmosphäre]] als Kondensationskerne und tragen zur [[Wolke]]nbildung bei.<ref>[[Alfred Wiedensohler]]: ''Partikelzählung in der Außenluft – eine Messaufgabe mit Zukunft.'' In: ''Gefahrstoffe – Reinhalt. Luft.'' 64, Nr. 7/8, 2004, {{ISSN|0949-8036}}, S. 313.</ref> | |||
* Bei der [[Partikelmessung|Messung von Partikeln]] mit dem [[Kondensationspartikelzähler]] wird die Eigenschaft der Partikel als Kondensationskern gezielt genutzt, um sie durch Kondensation zu vergrößern und für die zählende Optik sichtbar zu machen.<ref>VDI 3867 Blatt 2:2008-02 ''Messen von Partikeln in der Außenluft; Charakterisierung von Prüfaerosolen; Bestimmung der Partikelanzahlkonzentration und Anzahlgrößenverteilung; Kondensationspartikelzähler (CPC) (Measurement of particulate matter in ambient air; Methods for characterizing test aerosols; Determination of the particle number concentration and particle size distribution; Condensation Particle Counter (CPC)).'' Beuth Verlag, Berlin, S. 3–4.</ref> | |||
* Für die Herstellung von [[Prüfaerosol]]en (d. h. Aerosolen mit definierten Eigenschaften), die auf Kondensationsverfahren beruhen, werden Kondensationskerne verwendet.<ref>VDI 3491 Blatt 4:2018-03 ''Messen von Partikeln; Herstellungsverfahren für Prüfaerosole; Kondensationsverfahren (Measurement of particles; Methods for generating test aerosols; Condensation methods).'' Beuth Verlag, Berlin, S. 9–10.</ref> | |||
[[Datei:Storm Glass FitzRoy Sturmglas.JPG|mini|hochkant|Unterschiedliche Kristallformen in einem [[Sturmglas]] zeigen angeblich die Form des anstehenden Wetters an. Nach einer Theorie<ref>Hans Baumer: ''Sferics, die Entdeckung der Wetterstrahlung.'' Rowohlt, Reinbek bei Hamburg 1987, ISBN 3-498-00487-5, S. 162–175</ref> sollen dabei [[Sferics]] als Nukleationsursache das unterschiedliche Kristallwachstum anregen]] | |||
=== Kristallisationskeim === | |||
'''Kristallisationskeime''' oder '''Kristallisationskerne''' sind [[Dispersion (Chemie)|feindisperse]] oder [[makroskopisch]]e, feste [[Teilchen#Verwandte Begriffe|Partikel]] in einer [[fluid]]en [[Phase (Materie)|Phase]]. Sie erleichtern die [[Kristallisation]], also die Bildung von [[Kristall]]en, die sonst nur aus [[übersättigt]]en Medien möglich wäre. Dabei kann zwischen [[Erstarrung]]s-, [[Resublimation]]s- oder Aus[[fällung]]svorgängen unterschieden werden. | |||
==== Kristallisation aus Lösungen ==== | |||
Die Kristallisation aus [[Lösung (Chemie)|Lösungen]] sollte beginnen, sobald das [[Löslichkeit]]sprodukt der gelösten Substanzen überschritten ist. Dies wird meistens jedoch nicht beobachtet. Beim Aufbau einer neuen Phase muss nämlich beachtet werden, dass sich die zugehörige Änderung <math>\Delta G</math> der [[Gibbs-Energie|Freien Enthalpie]] aus zwei konkurrierenden Termen zusammensetzt: | |||
:<math>\Delta G = \Delta G_V + \Delta G_\sigma </math> | |||
* dem [[thermodynamisch]] begünstigten Volumenanteil <math>\Delta G_V</math>, den man sich bildlich als Zunahme [[Chemische Bindung|chemischer Bindungen]] vorstellen kann, | |||
* der [[Arbeit (Physik)|Arbeit]] <math>\Delta G_\sigma </math>, die aufgebracht werden muss, um eine neue [[Grenzfläche|Oberfläche]] zu bilden. | |||
Bei größeren Kristallen überwiegt der Volumenanteil, für sehr kleine Kristalle dagegen der Oberflächenterm, weshalb man hierbei von ''[[Kinetik (Chemie)|kinetisch]] gehemmtem Kristallwachstum'' spricht. Dies wird durch die Anwesenheit von Kristallisationskeimen umgangen. | |||
==== Kristallisation aus Schmelzen ==== | |||
In [[Schmelzen]] entstehen Kristallisationskeime am Beginn eines Erstarrungsvorgangs von kristallin aufgebauten [[Chemisches Element|Elementen]], [[Legierung]]en und [[Chemische Verbindung|Verbindungen]]. Sie bilden Ausgangspunkte für deren weitere Kristallisation. Eine Gruppe von [[Atom]]en, die beim Erreichen der [[Erstarrungstemperatur]] zufällig eine Anordnung im [[Kristallsystem]] des betreffenden Stoffes eingenommen hat, verbleibt in dieser Position unter Abgabe von [[thermische Energie|thermischer Energie]]. | |||
== Klassische Keimbildungstheorie == | == Klassische Keimbildungstheorie == | ||
Die klassische Keimbildungstheorie macht einige grundlegende, vereinfachende Annahmen, die eine Beschreibung des | Wegen ihrer großen technischen Relevanz werden Nukleationsprozesse seit dem Beginn des zwanzigsten Jahrhunderts systematisch untersucht. Substantielle Ergebnisse liegen bisher vor allem für den Phasenübergang gasförmig-flüssig, Kristallisation sowie für die Gefügeänderung in wenigen Metallen vor. Die hierfür aufgestellten Theorien werden mangels Alternative häufig auf die restlichen Systeme übertragen. | ||
Bis heute herrscht aufgrund ihrer einfachen Struktur die klassische Keimbildungstheorie (''classical nucleation theory'')<ref>M. Volmer and A. Weber: Tröpfchenbildung in Dämpfen, Z. Phys. Chem. (Leipzig) Bd. 119, S. 227, 1926</ref><ref>L. Farkas: Keimbildungsgeschwindigkeit in übersättigten Dämpfen, Zeitschr. f. physik. Chemie, Bd. 125, S. 236, 1927 [http://www.physik.uni-augsburg.de/theo1/hanggi/History/Farkas.pdf PDF]</ref><ref>R. Becker, W. Döring: Kinetische Behandlung der Keimbildung in übersättigten Dämpfen, Ann. Phys. Bd. 24, S. 719, 1935, {{DOI|10.1002/andp.19354160806}}</ref><ref>D. Kashchiev, Butterworth-Heinemann (Hrsg.): „Nucleation: Basic Theory With Applications“, 2000, ISBN 0-7506-4682-9</ref><ref>P. G. Debenedetti, Princeton University Press (Hrsg.): „Metastable Liquids: Concepts and Principles“, 1996</ref> vor, obwohl insbesondere für den gasförmig-flüssig-Übergang wiederholt gezeigt wurde, dass ihre Vorhersagen typischerweise um mehrere Größenordnungen(!) von der Realität abweichen, z. B. bei [[Argon]] um mehr als 20 Größenordnungen.<ref>Alexander Fladerer, Reinhard Strey: ''Homogeneous nucleation and droplet growth in supersaturated argon vapor: The cryogenic nucleation pulse chamber.'' In: ''The Journal of Chemical Physics.'' 124, 2006, S. 164710, {{DOI|10.1063/1.2186327}}.</ref><ref>A. Fladerer: „Keimbildung und Tröpfchenwachstum in übersättigtem Argon-Dampf: Konstruktion einer kryogenen Nukleationspulskammer“, Cuvillier-Verlag, Göttingen (2002), ISBN 3-89873-494-3. [http://kups.ub.uni-koeln.de/id/eprint/465 PDF]</ref> Solch große Abweichungen zwischen Theorie und Experiment sind nahezu einzigartig in der gegenwärtigen Naturwissenschaft. Dies ist umso erstaunlicher, als es sich im Wesentlichen um ein Problem der [[Klassische Physik|klassischen Physik]] handelt. | |||
Die klassische Keimbildungstheorie macht einige grundlegende, vereinfachende Annahmen, die eine Beschreibung des Prozesses ermöglichen. Ein Großteil dieser Näherungen lässt sich unter dem Begriff ‚Kapillaritätsnäherung‘ zusammenfassen: Mit dieser Näherung wird angenommen, dass auch die kleinsten ([[mikroskopisch]]en) Keime bereits die gleichen (makroskopischen) Eigenschaften der neuen Phase besitzen. | |||
Zur Veranschaulichung der klassischen Keimbildungstheorie wird im Folgenden das Beispiel der Kondensation eines Tröpfchens aus einer [[übersättigt]]en Gasphase verwendet. In diesem Fall wird der Prozess üblicherweise bei konstanter Temperatur betrachtet, und die treibende Kraft ist die Übersättigung. | |||
=== Thermodynamik === | |||
Bei einer übersättigten Gasphase ist bei gegebener [[absolute Temperatur|Temperatur]] <math>T</math> der aktuelle Druck <math>p</math> höher als der Gleichgewichts[[dampfdruck]] <math>p_\mathrm{eq}(T)</math>: | |||
::<math>p > p_\mathrm{eq}(T) \Leftrightarrow \frac{p}{p_\mathrm{eq}(T)} > 1</math> | |||
Die [[Reversibler Prozess|reversible]] Arbeit, die notwendig ist, um aus dieser übersättigten Gasphase ein flüssiges Tröpfchen zu formen, d. h. die Keimbildungsarbeit, lässt sich berechnen. Dazu wird ein Prozess bei konstantem Druck <math>p</math>, konstantem Volumen <math>V</math> und konstanter [[Teilchenzahl]] <math>N</math> betrachtet. Das relevante [[thermodynamisches Potential|thermodynamische Potential]] ist also die [[Gibbs-Energie|freie Gibbs-Energie]]: | |||
:<math>G = \mu N</math> | |||
mit dem [[Chemisches Potential|chemischen Potential]] <math>\mu</math>. | |||
Konkret für eine reine [[Dampf]]phase (Index v für engl. ''vapor'') ergibt sich: | |||
:<math>G_\mathrm{v} = \mu_\mathrm{v} N</math>. | :<math>G_\mathrm{v} = \mu_\mathrm{v} N</math>. | ||
Für ein System, das sowohl Dampf als auch ein flüssiges Tröpfchen (index l) | |||
:<math>G(n) = \mu_\mathrm{v} (N-n)+\mu_\mathrm{l} n+\sigma A(n)</math>, | Für ein System, das sowohl Dampf als auch ein flüssiges Tröpfchen (index l für engl. ''liquid'') aus <math>n</math> Teilchen enthält, ergibt sich: | ||
wobei <math>\sigma</math> die Oberflächenspannung eines Tröpfchens mit der Oberfläche <math>A(n)</math> ist. Die Keimbildungsarbeit für ein Tröpfchen der Größe <math>n</math> in der Gasphase ist | |||
:<math>\Delta G = G(n) - G_\mathrm{v} = -n \Delta \mu + \sigma A </math>. | :<math>G(n) = \mu_\mathrm{v} (N - n) + \mu_\mathrm{l} n + \sigma A(n)</math>, | ||
In dieser Gleichung ist <math>\Delta \mu = \mu_\mathrm{v} - \mu_\mathrm{l}</math> | |||
Die klassische Keimbildungstheorie macht | wobei <math>\sigma</math> die Oberflächenspannung eines Tröpfchens mit der Oberfläche <math>A(n)</math> ist. | ||
* Das flüssige Tröpfchen ist kugelförmig, inkompressibel und hat eine scharfe Grenzfläche. | |||
* Das flüssige Tröpfchen hat die gleiche Oberflächenspannung, Dichte und Dampfdruck wie die makroskopische (flache) flüssige Phase. | Die Keimbildungsarbeit für ein Tröpfchen der Größe <math>n</math> in der Gasphase ist die Differenz <math>\Delta G(n)</math> der freien Gibbs-Energie <math>G(n)</math> eines Systems, das ein Tröpfchen der Größe <math>n</math> ''und'' Dampf enthält, und derjenigen des reinen Dampfsystems <math>G_\mathrm{v} = G(n = 0)</math>: | ||
* Der Dampfdruck kann mit Hilfe des idealen Gasgesetzes beschrieben werden. | |||
Mit Hilfe dieser Annahmen | :<math>\begin{alignat}{2} | ||
:<math> | \Delta G &= G(n) &&- G_\mathrm{v}\\ | ||
&= -n \Delta \mu &&+ \sigma A | |||
\end{alignat}</math>. | |||
In dieser Gleichung ist <math>\Delta \mu = \mu_\mathrm{v} - \mu_\mathrm{l}</math> die Differenz der chemischen Potentiale des Dampfes und der Flüssigkeit. | |||
Die klassische Keimbildungstheorie macht eine ganze Reihe vereinfachender Annahmen: | |||
* Das flüssige Tröpfchen ist kugelförmig, [[inkompressibel]] und hat eine scharfe [[Grenzfläche]]. | |||
* Das flüssige Tröpfchen hat die gleiche Oberflächenspannung, [[Dichte]] und Dampfdruck wie die makroskopische (flache) flüssige Phase. | |||
* Der Dampfdruck kann mit Hilfe des [[ideales Gasgesetz|idealen Gasgesetzes]] beschrieben werden. | |||
Mit Hilfe dieser Annahmen und der [[Gibbs-Duhem-Gleichung]] lässt sich die Differenz der chemischen Potentiale berechnen: | |||
::<math>\begin{align} | |||
\Delta \mu &= k_\mathrm{B} T \ln\left(\frac{p}{p_\mathrm{eq}(T)}\right)\\ | |||
&= k_\mathrm{B} T \ln{S} | |||
\end{align}</math>. | |||
mit | |||
* der [[Boltzmann-Konstante]]n <math>k_\mathrm{B}</math> | |||
* der Übersättigung <math>S = p / p_\mathrm{eq}(T) > 1</math>. | |||
Auch die Oberfläche lässt sich berechnen: | |||
::<math>A(n) = 4 \pi r^2(n) = s_1 n^{2/3}</math> | |||
mit | |||
* dem Radius <math>r(n)</math> des Tröpfchens | |||
* dem mittleren Oberflächenbedarf <math>s_1 = (36 \pi v_\mathrm{l}^{2})^{1/3}</math> eines Teilchens (Moleküls) | |||
** dem mittleren Volumen <math>v_\mathrm{l}</math> eines Teilchens in der flüssigen Phase. | |||
Damit ergibt sich für die Keimbildungsarbeit | |||
:<math>\Delta G = -n k_\mathrm{B} T \ln S + \sigma s_1 n^{2/3}</math>. | :<math>\Delta G = -n k_\mathrm{B} T \ln S + \sigma s_1 n^{2/3}</math>. | ||
[[Datei:CNT barrier.png| | Der erste Term, auch Volumenterm genannt, ist proportional zu <math>n</math>. Er stellt den Gewinn (daher negatives Vorzeichen) an Energie dar, der beim Übergang eines Moleküls aus der metastabilen Dampfphase in die stabile flüssige Phase auftritt. | ||
Der zweite Term ist die Arbeit, die aufgebracht werden muss (daher positives Vorzeichen), um die Oberfläche eines solchen flüssigen Tröpfchens zu formen. Er ist proportional zu <math>n^{2/3}</math>. | |||
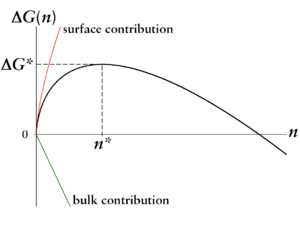
Bei <math>S>1</math> – nur für diesen Fall kann Keimbildung einsetzen – dominiert der Oberflächenterm für kleine Teilchenzahlen bzw. Tröpfchengrößen. Ab einer kritischen Tröpfchengröße <math>n^{*}</math> gewinnt der Volumenterm Oberhand. Das Maximum <math>\Delta G^{*}</math> ist die Keimbildungsarbeit, die aufgebracht werden muss, um ein Tröpfchen der kritischen Größe zu bilden. Dies ergibt das gezeigte Bild einer Barriere in der freien Energie <math>\Delta G(n)</math>. | |||
[[Datei:CNT barrier.png|mini|300px|Klassische Keimbildungstheorie: Keimbildungsarbeit als Funktion der Tröpfchengröße; rote Linie: Beitrag des Oberflächenterms, grüne Linie: ... des Volumenterms]] | |||
Die kritische Größe und die kritische Keimbildungsarbeit sind die bestimmenden Größen der Keimbildung: | |||
* Tröpfchen kleiner als <math>n^{*}</math> haben eine höhere Wahrscheinlichkeit, wieder zu [[verdampfen]] als weiter zu wachsen, da für sie das Verdampfen mit einem ''Gewinn'' an freier Gibbs-Energie verbunden ist (Bewegung nach unten auf der Kurve). | |||
* Nur Tröpfchen größer als <math>n^{*}</math> haben eine höhere Wahrscheinlichkeit, weiter zu wachsen als zu verdampfen, und können damit als Keime der neuen Phase dienen. | |||
Damit ist verständlich, warum eine Substanz für längere Zeit metastabil gehalten werden kann: Obwohl die neue Phase (in unserem Beispiel die flüssige) die thermodynamisch stabile Phase ist, muss der Prozess zunächst einige energetisch ungünstige Schritte durchlaufen, um die Barriere zu erklimmen. | |||
Die Barriere und die kritische Keimgröße nach der klassischen Keimbildungstheorie sind: | |||
:<math>\Delta G^{*} = \frac{16\pi}{3}\frac{v_{l}^{2}\sigma^{3}}{(k_\mathrm{B}T\ln S)^{2}}</math> | :<math>\Delta G^{*} = \frac{16\pi}{3}\frac{v_{l}^{2}\sigma^{3}}{(k_\mathrm{B}T\ln S)^{2}}</math> | ||
und | und | ||
:<math>n^{*} = 2\Delta G^{*}/k_\mathrm{B}T\ln S</math>. | |||
:<math> | |||
== | === Kinetik === | ||
Um nun eine Keimbildungsrate <math>J</math> zu berechnen, also die Anzahl der pro Volumen und Zeit gebildeten Keime, muss auch die [[Kinetik (Chemie)|Kinetik]] der Keimbildung betrachtet werden. Die stationäre Keimbildungsrate wird üblicherweise in Form eines [[Arrhenius-Gleichung|Arrhenius-Ansatzes]] berechnet: | |||
:<math>J = K e^{-\Delta G^{*}/k_\mathrm{B}T}</math> | |||
Der Vorfaktor <math>K</math> wird üblicherweise der kinetische Vorfaktor genannt, auf ihn wird hier jedoch nicht näher eingegangen. | |||
Üblicherweise hat die Höhe <math>\Delta G^{*}</math> der Barriere aufgrund der exponentiellen Abhängigkeit einen wesentlich größeren und entscheidenden Einfluss. | |||
== | === Homogene Keimbildung === | ||
Erfolgt die Nukleation im freien Raum, also durch ein statisches Zusammentreffen ''gleicher'' Teilchen, so spricht man von einer homogenen Keimbildung. | |||
Hierzu ist es notwendig, dass sich im Falle der Kondensation ausreichend viele und langsame Teilchen ohne weitere Hilfe zu größeren Strukturen zusammenfinden. Langsame Teilchen können durch das gleichzeitige Zusammentreffen von mehr als zwei Teilchen ([[Dreierstoß]]) entstehen. Hierbei nimmt ein Teilchen einen Großteil der [[kinetische Energie|kinetischen Energie]] auf und hinterlässt zwei langsame Teilchen. Die Übersättigung ist dabei ungefähr proportional zur Wahrscheinlichkeit eines derartigen Dreierstoßes, der zur Nukleation führt. Abhängig von dem betrachteten System können daher thermodynamisch metastabile Systeme sehr lange in diesem Zustand verharren. | |||
== | === Heterogene Keimbildung === | ||
Im Gegensatz zur homogenen Keimbildung benötigt man bei der heterogenen Keimbildung nur sehr geringe Übersättigungen von oft unter einem Prozent. Diese Form der Kondensation erfolgt im Fall der Kondensation an bereits existierenden Oberflächen (heterogen: an ''andersartigen'' Teilchen), also im Regelfall an festen Partikeln, die in der Gasphase schweben, den [[Kondensationskern]]en bzw. [[Aerosol]]teilchen. Diese fungieren in Bezug auf das jeweilige Gas als eine Art Teilchenfänger, wobei im Wesentlichen der Radius und die chemischen Eigenschaften des Partikels bestimmen, wie gut die Gasteilchen an ihm haften. Analog gilt dies auch für Oberflächen nicht partikulärer Körper, wobei man dann von einem ''Beschlag'' spricht. In jedem Falle wirken heterogene Teilchen oder Oberflächen als ein Katalysator für die Keimbildung, indem sie die Keimbildungsbarriere deutlich verringern. | |||
* [ | == Weblinks == | ||
* | {{Wiktionary}} | ||
* Yvonne Rückl: ''Die Nukleation'', Unterlagen der Universität Bayreuth [http://daten.didaktikchemie.uni-bayreuth.de/umat/nukleation/Nukleation.pdf PDF-Datei] | |||
* [ | * Günter Jakob Lauth, Jürgen Kowalczyk: ''Einführung in die Physik und Chemie der Grenzflächen und Kolloide.'' Springer-Verlag, 2015, ISBN 3662470187 S. 79, Kapitel Nukleationstheorie ({{Google Buch|BuchID=VwycCgAAQBAJ|Seite=76}}). | ||
* [ | * [https://sciencev2.orf.at/stories/1701384/index.html Pollen lassen Wolken gefrieren], science.ORF.at/APA, | ||
* [https://www.eepybird.com/featured-video/the-extreme-diet-coke-mentos-experiments/ The Extreme Diet Coke & Mentos Experiments] ''(en)'' – angewandte Nukleation | |||
== Einzelnachweise == | == Einzelnachweise == | ||
<references /> | <references /> | ||
== | {{Normdaten|TYP=s|GND=4164925-4}} | ||
[[Kategorie:Thermodynamik]] | [[Kategorie:Thermodynamik]] | ||
[[Kategorie:Niederschlag]] | |||
[[Kategorie:Wolke]] | |||
[[Kategorie:Festkörperchemie]] | |||
[[Kategorie:Kristallzüchtung]] | |||
[[Kategorie:Kristallographie]] | |||
[[Kategorie:Wikipedia:Artikel mit Video]] | |||
Aktuelle Version vom 8. Februar 2022, 12:43 Uhr
Keimbildung oder Nukleation ist der grundlegende Prozess, bei dem sich an einer Keimstelle ein Nukleationskeim bildet, der als "Startkomponente" einen Phasenübergang erster Ordnung einleitet.
Beispiele für einen Phasenübergang sind
- die Kondensation von Dampf zu Flüssigkeit
- sowie umgekehrt: die Blasenbildung beim Übergang von der flüssigen zur gasförmigen Phase
- der Beginn einer Kristallisation
- Gefrieren einer Flüssigkeit
- Abscheidung durch Resublimation direkt aus der Gasphase
- Bildung von kristallinen Festkörpern aus einer übersättigten Lösung
- Kristallitbildung bei Abkühlung einer Schmelze (beispielsweise Bainitbildung)
- Entmischungsvorgänge zweier flüssiger Phasen.
- weitere Phasenübergangsformen siehe Phasenübergang #Weitere Klassifikationen.
Bei stärkerer Übersättigung oder Unterkühlung kann die Keimbildung spontan erfolgen.[1] Lokale Dichtefluktuationen (statistische Schwankungen (=Fluktuationen) des Aufenthaltsortes der Moleküle nach Mikroclusterbildung auf molekularer Ebene) führen dabei zu Dichte- und Druckunterschieden (wie sie auch bei der Thermokonvektion auftreten) und so zur Keimbildung.
Auch die allgegenwärtige kosmische Strahlung erzeugt stoßionisierte Moleküle und bildet so (wie in einer Nebelkammer) Kondensationskeime für Nebel- und Wolkenbildung.
Allgemeines
Wesentliches Merkmal der Keimbildung ist, dass die neue, bei den gegebenen Bedingungen thermodynamisch stabile Phase, zunächst durch Keime aus der alten, metastabilen Phase gebildet wird. Unter einem einzelnen Keim versteht man hierbei einen kleinen in der Regel nur wenige Nanometer umfassenden räumlich homogenen Bereich der neuen Phase innerhalb der alten Phase.
Die Bildung dieser typischerweise nur nanometergroßen Keime ist zunächst kinetisch gehemmt (bei kinetischer Hemmung ist die Reaktionsgeschwindigkeit sehr klein und deswegen eine Aktivierungsenergie nötig;[2] siehe dazu auch Sterische Hinderung). Flüssigkeiten lassen sich unterkühlen und überhitzen. Der Grund für diese Hemmung liegt in der Arbeit, die aufgebracht werden muss, um die gekrümmte Oberfläche eines kleinsten Keims (z. B. ein kugelförmiges Tröpfchen) der neuen Phase zu bilden. Für kleinste Tröpfchen oder Kristalle ist diese Oberflächenarbeit größer als der Energiegewinn aus dem Übergang in die neue, stabile Phase. Die daraus entstehende freie Energiebarriere nennt man Keimbildungsbarriere und die Arbeit, die aufgebracht werden muss, um diese Barriere zu überwinden, Keimbildungsarbeit (vgl. unten Thermodynamik). Der Bereich des Phasendiagramms, in dem die Keime unterhalb der kritischen Keimgröße bleiben, wird Ostwald-Miers-Bereich genannt.
Sind jedoch einmal Keime, die größer sind als die kritische Keimgröße, aus thermischen Fluktuationen gebildet, so wachsen sie schnell zur makroskopischen Phase an. Keimbildung kann damit auch als Prototyp eines aktivierten Prozesses verstanden werden.
Die Nukleationsrate oder Keimbildungsrate beschreibt, wie viele Keime der neuen Phase pro Volumen- und Zeiteinheit gebildet werden. Diese Keimbildungsrate hängt stark exponentiell von der Keimbildungsarbeit ab: je höher die Keimbildungsarbeit und damit die Barriere zur Keimbildung, desto niedriger die Rate (vgl. unten Kinetik).
Auftreten
Keimbildung ist ein allgegenwärtiger Prozess. Beispielsweise bildet Rauheit an einer Behälterwandung Keimstellen für ausgasendes CO2. Feinstaub und sonstiger Schwebstaub können Kondensationskeime bei der Bildung von Nebel- oder Regenwolken liefern. In einem Wärmekissen liefert ein umgeknicktes Metallplättchen die nötigen Kristallisationskeime.
Für die Industrie ist die Kenntnis der Keimbildungskinetik von höchstem Interesse, z. B. um den Tropfenschlag in Gasturbinen oder den Siedeverzug in Verdampfern zu verhindern oder um die Bildung des Kondensstreifens bei Düsenflugzeugen zu kontrollieren. Die Nukleation spielt darüber hinaus eine zentrale Rolle in der Verfahrenstechnik von Polymeren, Legierungen sowie manchen Keramiken, aber auch bei der Kontrolle bzw. Verhinderung der Kristallisation (z. B. bei Halbleitermaterialien, metallischen Gläsern oder Honig).
Electrofreezing ist ein Verfahren, durch das die Kristallisation von Wasser und anderen Flüssigkeiten beim Gefrierprozess gezielt durch das Anlegen eines elektrischen Feldes ausgelöst werden kann. Dieses physikalische Phänomen ist seit 1861 bekannt.

Kondensationskeime
Ein Kondensationskeim oder auch Kondensationskern erleichtert die Keimbildung und die folgende Kondensation eines gasförmigen Stoffes. Ein solcher Keim kann eine Verschmutzung sein, wie ein Staub-, Salz- oder Rußpartikel, oder ionisierte Gasmoleküle, wie bei der Nebelkammer. Der Nachweis von Kondensationskernen gelang P. J. Coulier im Jahr 1875.[4]
Beispiele
- Aerosolpartikel, die bestimmte chemische und physikalische Eigenschaften besitzen, fungieren in der Erdatmosphäre als Kondensationskerne und tragen zur Wolkenbildung bei.[5]
- Bei der Messung von Partikeln mit dem Kondensationspartikelzähler wird die Eigenschaft der Partikel als Kondensationskern gezielt genutzt, um sie durch Kondensation zu vergrößern und für die zählende Optik sichtbar zu machen.[6]
- Für die Herstellung von Prüfaerosolen (d. h. Aerosolen mit definierten Eigenschaften), die auf Kondensationsverfahren beruhen, werden Kondensationskerne verwendet.[7]
Kristallisationskeim
Kristallisationskeime oder Kristallisationskerne sind feindisperse oder makroskopische, feste Partikel in einer fluiden Phase. Sie erleichtern die Kristallisation, also die Bildung von Kristallen, die sonst nur aus übersättigten Medien möglich wäre. Dabei kann zwischen Erstarrungs-, Resublimations- oder Ausfällungsvorgängen unterschieden werden.
Kristallisation aus Lösungen
Die Kristallisation aus Lösungen sollte beginnen, sobald das Löslichkeitsprodukt der gelösten Substanzen überschritten ist. Dies wird meistens jedoch nicht beobachtet. Beim Aufbau einer neuen Phase muss nämlich beachtet werden, dass sich die zugehörige Änderung $ \Delta G $ der Freien Enthalpie aus zwei konkurrierenden Termen zusammensetzt:
- $ \Delta G=\Delta G_{V}+\Delta G_{\sigma } $
- dem thermodynamisch begünstigten Volumenanteil $ \Delta G_{V} $, den man sich bildlich als Zunahme chemischer Bindungen vorstellen kann,
- der Arbeit $ \Delta G_{\sigma } $, die aufgebracht werden muss, um eine neue Oberfläche zu bilden.
Bei größeren Kristallen überwiegt der Volumenanteil, für sehr kleine Kristalle dagegen der Oberflächenterm, weshalb man hierbei von kinetisch gehemmtem Kristallwachstum spricht. Dies wird durch die Anwesenheit von Kristallisationskeimen umgangen.
Kristallisation aus Schmelzen
In Schmelzen entstehen Kristallisationskeime am Beginn eines Erstarrungsvorgangs von kristallin aufgebauten Elementen, Legierungen und Verbindungen. Sie bilden Ausgangspunkte für deren weitere Kristallisation. Eine Gruppe von Atomen, die beim Erreichen der Erstarrungstemperatur zufällig eine Anordnung im Kristallsystem des betreffenden Stoffes eingenommen hat, verbleibt in dieser Position unter Abgabe von thermischer Energie.
Klassische Keimbildungstheorie
Wegen ihrer großen technischen Relevanz werden Nukleationsprozesse seit dem Beginn des zwanzigsten Jahrhunderts systematisch untersucht. Substantielle Ergebnisse liegen bisher vor allem für den Phasenübergang gasförmig-flüssig, Kristallisation sowie für die Gefügeänderung in wenigen Metallen vor. Die hierfür aufgestellten Theorien werden mangels Alternative häufig auf die restlichen Systeme übertragen.
Bis heute herrscht aufgrund ihrer einfachen Struktur die klassische Keimbildungstheorie (classical nucleation theory)[9][10][11][12][13] vor, obwohl insbesondere für den gasförmig-flüssig-Übergang wiederholt gezeigt wurde, dass ihre Vorhersagen typischerweise um mehrere Größenordnungen(!) von der Realität abweichen, z. B. bei Argon um mehr als 20 Größenordnungen.[14][15] Solch große Abweichungen zwischen Theorie und Experiment sind nahezu einzigartig in der gegenwärtigen Naturwissenschaft. Dies ist umso erstaunlicher, als es sich im Wesentlichen um ein Problem der klassischen Physik handelt.
Die klassische Keimbildungstheorie macht einige grundlegende, vereinfachende Annahmen, die eine Beschreibung des Prozesses ermöglichen. Ein Großteil dieser Näherungen lässt sich unter dem Begriff ‚Kapillaritätsnäherung‘ zusammenfassen: Mit dieser Näherung wird angenommen, dass auch die kleinsten (mikroskopischen) Keime bereits die gleichen (makroskopischen) Eigenschaften der neuen Phase besitzen.
Zur Veranschaulichung der klassischen Keimbildungstheorie wird im Folgenden das Beispiel der Kondensation eines Tröpfchens aus einer übersättigten Gasphase verwendet. In diesem Fall wird der Prozess üblicherweise bei konstanter Temperatur betrachtet, und die treibende Kraft ist die Übersättigung.
Thermodynamik
Bei einer übersättigten Gasphase ist bei gegebener Temperatur $ T $ der aktuelle Druck $ p $ höher als der Gleichgewichtsdampfdruck $ p_{\mathrm {eq} }(T) $:
- $ p>p_{\mathrm {eq} }(T)\Leftrightarrow {\frac {p}{p_{\mathrm {eq} }(T)}}>1 $
Die reversible Arbeit, die notwendig ist, um aus dieser übersättigten Gasphase ein flüssiges Tröpfchen zu formen, d. h. die Keimbildungsarbeit, lässt sich berechnen. Dazu wird ein Prozess bei konstantem Druck $ p $, konstantem Volumen $ V $ und konstanter Teilchenzahl $ N $ betrachtet. Das relevante thermodynamische Potential ist also die freie Gibbs-Energie:
- $ G=\mu N $
mit dem chemischen Potential $ \mu $.
Konkret für eine reine Dampfphase (Index v für engl. vapor) ergibt sich:
- $ G_{\mathrm {v} }=\mu _{\mathrm {v} }N $.
Für ein System, das sowohl Dampf als auch ein flüssiges Tröpfchen (index l für engl. liquid) aus $ n $ Teilchen enthält, ergibt sich:
- $ G(n)=\mu _{\mathrm {v} }(N-n)+\mu _{\mathrm {l} }n+\sigma A(n) $,
wobei $ \sigma $ die Oberflächenspannung eines Tröpfchens mit der Oberfläche $ A(n) $ ist.
Die Keimbildungsarbeit für ein Tröpfchen der Größe $ n $ in der Gasphase ist die Differenz $ \Delta G(n) $ der freien Gibbs-Energie $ G(n) $ eines Systems, das ein Tröpfchen der Größe $ n $ und Dampf enthält, und derjenigen des reinen Dampfsystems $ G_{\mathrm {v} }=G(n=0) $:
- $ {\begin{alignedat}{2}\Delta G&=G(n)&&-G_{\mathrm {v} }\\&=-n\Delta \mu &&+\sigma A\end{alignedat}} $.
In dieser Gleichung ist $ \Delta \mu =\mu _{\mathrm {v} }-\mu _{\mathrm {l} } $ die Differenz der chemischen Potentiale des Dampfes und der Flüssigkeit.
Die klassische Keimbildungstheorie macht eine ganze Reihe vereinfachender Annahmen:
- Das flüssige Tröpfchen ist kugelförmig, inkompressibel und hat eine scharfe Grenzfläche.
- Das flüssige Tröpfchen hat die gleiche Oberflächenspannung, Dichte und Dampfdruck wie die makroskopische (flache) flüssige Phase.
- Der Dampfdruck kann mit Hilfe des idealen Gasgesetzes beschrieben werden.
Mit Hilfe dieser Annahmen und der Gibbs-Duhem-Gleichung lässt sich die Differenz der chemischen Potentiale berechnen:
- $ {\begin{aligned}\Delta \mu &=k_{\mathrm {B} }T\ln \left({\frac {p}{p_{\mathrm {eq} }(T)}}\right)\\&=k_{\mathrm {B} }T\ln {S}\end{aligned}} $.
mit
- der Boltzmann-Konstanten $ k_{\mathrm {B} } $
- der Übersättigung $ S=p/p_{\mathrm {eq} }(T)>1 $.
Auch die Oberfläche lässt sich berechnen:
- $ A(n)=4\pi r^{2}(n)=s_{1}n^{2/3} $
mit
- dem Radius $ r(n) $ des Tröpfchens
- dem mittleren Oberflächenbedarf $ s_{1}=(36\pi v_{\mathrm {l} }^{2})^{1/3} $ eines Teilchens (Moleküls)
- dem mittleren Volumen $ v_{\mathrm {l} } $ eines Teilchens in der flüssigen Phase.
Damit ergibt sich für die Keimbildungsarbeit
- $ \Delta G=-nk_{\mathrm {B} }T\ln S+\sigma s_{1}n^{2/3} $.
Der erste Term, auch Volumenterm genannt, ist proportional zu $ n $. Er stellt den Gewinn (daher negatives Vorzeichen) an Energie dar, der beim Übergang eines Moleküls aus der metastabilen Dampfphase in die stabile flüssige Phase auftritt.
Der zweite Term ist die Arbeit, die aufgebracht werden muss (daher positives Vorzeichen), um die Oberfläche eines solchen flüssigen Tröpfchens zu formen. Er ist proportional zu $ n^{2/3} $.
Bei $ S>1 $ – nur für diesen Fall kann Keimbildung einsetzen – dominiert der Oberflächenterm für kleine Teilchenzahlen bzw. Tröpfchengrößen. Ab einer kritischen Tröpfchengröße $ n^{*} $ gewinnt der Volumenterm Oberhand. Das Maximum $ \Delta G^{*} $ ist die Keimbildungsarbeit, die aufgebracht werden muss, um ein Tröpfchen der kritischen Größe zu bilden. Dies ergibt das gezeigte Bild einer Barriere in der freien Energie $ \Delta G(n) $.
Die kritische Größe und die kritische Keimbildungsarbeit sind die bestimmenden Größen der Keimbildung:
- Tröpfchen kleiner als $ n^{*} $ haben eine höhere Wahrscheinlichkeit, wieder zu verdampfen als weiter zu wachsen, da für sie das Verdampfen mit einem Gewinn an freier Gibbs-Energie verbunden ist (Bewegung nach unten auf der Kurve).
- Nur Tröpfchen größer als $ n^{*} $ haben eine höhere Wahrscheinlichkeit, weiter zu wachsen als zu verdampfen, und können damit als Keime der neuen Phase dienen.
Damit ist verständlich, warum eine Substanz für längere Zeit metastabil gehalten werden kann: Obwohl die neue Phase (in unserem Beispiel die flüssige) die thermodynamisch stabile Phase ist, muss der Prozess zunächst einige energetisch ungünstige Schritte durchlaufen, um die Barriere zu erklimmen.
Die Barriere und die kritische Keimgröße nach der klassischen Keimbildungstheorie sind:
- $ \Delta G^{*}={\frac {16\pi }{3}}{\frac {v_{l}^{2}\sigma ^{3}}{(k_{\mathrm {B} }T\ln S)^{2}}} $
und
- $ n^{*}=2\Delta G^{*}/k_{\mathrm {B} }T\ln S $.
Kinetik
Um nun eine Keimbildungsrate $ J $ zu berechnen, also die Anzahl der pro Volumen und Zeit gebildeten Keime, muss auch die Kinetik der Keimbildung betrachtet werden. Die stationäre Keimbildungsrate wird üblicherweise in Form eines Arrhenius-Ansatzes berechnet:
- $ J=Ke^{-\Delta G^{*}/k_{\mathrm {B} }T} $
Der Vorfaktor $ K $ wird üblicherweise der kinetische Vorfaktor genannt, auf ihn wird hier jedoch nicht näher eingegangen. Üblicherweise hat die Höhe $ \Delta G^{*} $ der Barriere aufgrund der exponentiellen Abhängigkeit einen wesentlich größeren und entscheidenden Einfluss.
Homogene Keimbildung
Erfolgt die Nukleation im freien Raum, also durch ein statisches Zusammentreffen gleicher Teilchen, so spricht man von einer homogenen Keimbildung.
Hierzu ist es notwendig, dass sich im Falle der Kondensation ausreichend viele und langsame Teilchen ohne weitere Hilfe zu größeren Strukturen zusammenfinden. Langsame Teilchen können durch das gleichzeitige Zusammentreffen von mehr als zwei Teilchen (Dreierstoß) entstehen. Hierbei nimmt ein Teilchen einen Großteil der kinetischen Energie auf und hinterlässt zwei langsame Teilchen. Die Übersättigung ist dabei ungefähr proportional zur Wahrscheinlichkeit eines derartigen Dreierstoßes, der zur Nukleation führt. Abhängig von dem betrachteten System können daher thermodynamisch metastabile Systeme sehr lange in diesem Zustand verharren.
Heterogene Keimbildung
Im Gegensatz zur homogenen Keimbildung benötigt man bei der heterogenen Keimbildung nur sehr geringe Übersättigungen von oft unter einem Prozent. Diese Form der Kondensation erfolgt im Fall der Kondensation an bereits existierenden Oberflächen (heterogen: an andersartigen Teilchen), also im Regelfall an festen Partikeln, die in der Gasphase schweben, den Kondensationskernen bzw. Aerosolteilchen. Diese fungieren in Bezug auf das jeweilige Gas als eine Art Teilchenfänger, wobei im Wesentlichen der Radius und die chemischen Eigenschaften des Partikels bestimmen, wie gut die Gasteilchen an ihm haften. Analog gilt dies auch für Oberflächen nicht partikulärer Körper, wobei man dann von einem Beschlag spricht. In jedem Falle wirken heterogene Teilchen oder Oberflächen als ein Katalysator für die Keimbildung, indem sie die Keimbildungsbarriere deutlich verringern.
Weblinks
- Yvonne Rückl: Die Nukleation, Unterlagen der Universität Bayreuth PDF-Datei
- Günter Jakob Lauth, Jürgen Kowalczyk: Einführung in die Physik und Chemie der Grenzflächen und Kolloide. Springer-Verlag, 2015, ISBN 3662470187 S. 79, Kapitel Nukleationstheorie (eingeschränkte Vorschau in der Google-Buchsuche).
- Pollen lassen Wolken gefrieren, science.ORF.at/APA,
- The Extreme Diet Coke & Mentos Experiments (en) – angewandte Nukleation
Einzelnachweise
- ↑ VDI 3491 Blatt 4:2018-03 Messen von Partikeln; Herstellungsverfahren für Prüfaerosole; Kondensationsverfahren (Measurement of particles; Methods for generating test aerosols; Condensation methods). Beuth Verlag, Berlin, S. 4.
- ↑ Hans Peter Latscha, Helmut Alfons Klein: Anorganische Chemie. Springer-Verlag, 2013, ISBN 3662057573 S. 243 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Aerosol und Wolkenphysik, S. 5
- ↑ Carsten Möhlmann: Staubmesstechnik - damals bis heute. In: Gefahrstoffe – Reinhalt. Luft. 65, Nr. 5, 2005, ISSN 0949-8036, S. 191–194. (PDF; 335 kB)
- ↑ Alfred Wiedensohler: Partikelzählung in der Außenluft – eine Messaufgabe mit Zukunft. In: Gefahrstoffe – Reinhalt. Luft. 64, Nr. 7/8, 2004, ISSN 0949-8036, S. 313.
- ↑ VDI 3867 Blatt 2:2008-02 Messen von Partikeln in der Außenluft; Charakterisierung von Prüfaerosolen; Bestimmung der Partikelanzahlkonzentration und Anzahlgrößenverteilung; Kondensationspartikelzähler (CPC) (Measurement of particulate matter in ambient air; Methods for characterizing test aerosols; Determination of the particle number concentration and particle size distribution; Condensation Particle Counter (CPC)). Beuth Verlag, Berlin, S. 3–4.
- ↑ VDI 3491 Blatt 4:2018-03 Messen von Partikeln; Herstellungsverfahren für Prüfaerosole; Kondensationsverfahren (Measurement of particles; Methods for generating test aerosols; Condensation methods). Beuth Verlag, Berlin, S. 9–10.
- ↑ Hans Baumer: Sferics, die Entdeckung der Wetterstrahlung. Rowohlt, Reinbek bei Hamburg 1987, ISBN 3-498-00487-5, S. 162–175
- ↑ M. Volmer and A. Weber: Tröpfchenbildung in Dämpfen, Z. Phys. Chem. (Leipzig) Bd. 119, S. 227, 1926
- ↑ L. Farkas: Keimbildungsgeschwindigkeit in übersättigten Dämpfen, Zeitschr. f. physik. Chemie, Bd. 125, S. 236, 1927 PDF
- ↑ R. Becker, W. Döring: Kinetische Behandlung der Keimbildung in übersättigten Dämpfen, Ann. Phys. Bd. 24, S. 719, 1935, doi:10.1002/andp.19354160806
- ↑ D. Kashchiev, Butterworth-Heinemann (Hrsg.): „Nucleation: Basic Theory With Applications“, 2000, ISBN 0-7506-4682-9
- ↑ P. G. Debenedetti, Princeton University Press (Hrsg.): „Metastable Liquids: Concepts and Principles“, 1996
- ↑ Alexander Fladerer, Reinhard Strey: Homogeneous nucleation and droplet growth in supersaturated argon vapor: The cryogenic nucleation pulse chamber. In: The Journal of Chemical Physics. 124, 2006, S. 164710, doi:10.1063/1.2186327.
- ↑ A. Fladerer: „Keimbildung und Tröpfchenwachstum in übersättigtem Argon-Dampf: Konstruktion einer kryogenen Nukleationspulskammer“, Cuvillier-Verlag, Göttingen (2002), ISBN 3-89873-494-3. PDF