Gradientenfeld: Unterschied zwischen den Versionen
imported>Jobu0101 K (Satzzeichen an die richtige Stelle gerückt) |
imported>ZabesBot K (Bot: Räume alte Interwikilinks auf) |
||
| Zeile 1: | Zeile 1: | ||
{{Dieser Artikel|behandelt die Bedeutung des Wortes in der Mathematik und der Physik. Der Begriff wird aber auch bei der Beschreibung von physikalischen Versuchsaufbauten im Sinne eines Feldes verwendet, dessen Feldstärke sich kontinuierlich ändert; siehe z. B. [[Magnetic Particle Imaging]], [[Antiproton Decelerator#AEGIS (AD-6)|AEGIS-Experiment]]}} | {{Dieser Artikel|behandelt die Bedeutung des Wortes in der Mathematik und der Physik. Der Begriff wird aber auch bei der Beschreibung von physikalischen Versuchsaufbauten im Sinne eines Feldes verwendet, dessen Feldstärke sich kontinuierlich ändert; siehe z. B. [[Magnetic Particle Imaging]], [[Antiproton Decelerator#AEGIS (AD-6)|AEGIS-Experiment]]}} | ||
Ein '''Gradientenfeld''' ist ein [[Vektorfeld]], das aus einem [[Skalarfeld]] durch [[Differentiation]] nach dem Ort abgeleitet wurde, bzw. – kürzer formuliert – der [[Gradient (Mathematik)|Gradient]] des Skalarfelds. | Ein '''Gradientenfeld''' oder '''konservatives Feld''' ist ein [[Vektorfeld]], das aus einem [[Skalarfeld]] durch [[Differentiation]] nach dem Ort abgeleitet wurde, bzw. – kürzer formuliert – der [[Gradient (Mathematik)|Gradient]] des Skalarfelds. Dieses Vektorfeld hat die Eigenschaft, dass sein [[Kurvenintegral]] wegunabhängig ist. | ||
Zur besseren Abgrenzung zwischen dem ''Gradienten als mathematischem Operator'' und dem ''Resultat seiner Anwendung'' bezeichnen manche Autoren die Vektoren, aus denen sich Gradientenfelder zusammensetzen, auch als '''Gradientvektoren''',<ref name="Grimsehl 1">Grimsehl: ''Lehrbuch der Physik, Bd. I.'' Leipzig 1954, S. 579.</ref> andere dagegen mit Blick auf die Potentiale, aus denen sie sich herleiten, als '''Potential''vektoren''''' <ref name="KEM 547">W. Gellert, H. Küstner, M. Hellwich, H. Kästner: ''Kleine Enzyklopädie Mathematik.'' Leipzig 1970, S. 547.</ref>. | Zur besseren Abgrenzung zwischen dem ''Gradienten als mathematischem Operator'' und dem ''Resultat seiner Anwendung'' bezeichnen manche Autoren die Vektoren, aus denen sich Gradientenfelder zusammensetzen, auch als '''Gradientvektoren''',<ref name="Grimsehl 1">Grimsehl: ''Lehrbuch der Physik, Bd. I.'' Leipzig 1954, S. 579.</ref> andere dagegen mit Blick auf die Potentiale, aus denen sie sich herleiten, als '''Potential''vektoren'''''<ref name="KEM 547">W. Gellert, H. Küstner, M. Hellwich, H. Kästner: ''Kleine Enzyklopädie Mathematik.'' Leipzig 1970, S. 547.</ref>. | ||
Analog verwendet die überwiegende Zahl der Autoren den Begriff '''Potential''feld''''' nicht für das skalare Feld des Potentials selbst, sondern das sich aus ihm ableitende Gradientenfeld <ref>[http://www.math.uni-kiel.de/geometrie/klein/ingws9/mo1412.pdf ''§4 Potentialfelder.''] (PDF; 1, | Analog verwendet die überwiegende Zahl der Autoren den Begriff '''Potential''feld''''' nicht für das skalare Feld des Potentials selbst, sondern das sich aus ihm ableitende Gradientenfeld<ref>[http://www.math.uni-kiel.de/geometrie/klein/ingws9/mo1412.pdf ''§4 Potentialfelder.''] (PDF; 1,8 MB) In: ''Mathematik für Ingenieure III.'' WS 2009/2010, Universität Kiel.</ref><ref>Albert Fetzer, Heiner Fränkel: ''Mathematik 2: Lehrbuch für ingenieurwissenschaftliche Studiengänge.'' Springer, Berlin/Heidelberg, S. 322.</ref>. | ||
== Definition | == Definition == | ||
Es gibt mehrere äquivalente Definitionen: | |||
:<math>\vec F(\vec r) = \vec \nabla \Phi(\vec r)</math> | # ''Ein Vektorfeld <math>\vec F \colon \vec r \mapsto \vec F(\vec r)</math> heißt Gradientenfeld, wenn es ein [[Skalarfeld]] <math>\Phi \colon \vec r \mapsto \Phi(\vec r)</math> gibt, sodass gilt:'' | ||
#:''<math>\vec F(\vec r) = \vec \nabla \Phi(\vec r)</math>'' | |||
# ''Das [[Kurvenintegral]] ist wegunabhängig: Der Wert des Kurvenintegrals entlang einer beliebigen Kurve <math>S</math> innerhalb des Feldes ist nur von ihrem Anfangs- und Endpunkt abhängig, nicht dagegen von ihrer [[Länge (Mathematik)|Länge]].'' | |||
# ''Kurvenintegrale über eine beliebige geschlossene Randkurve <math>S</math> ergeben immer Null:'' | |||
#:''<math>\oint_S \vec F(\vec r)\,\mathrm d \vec r = 0</math>'' | |||
Hier wird mit <math>\vec \nabla</math> der [[Gradient (Mathematik)|Gradient]] bezeichnet. <math>\Phi</math> nennt man das zu <math>\vec F</math> gehörige [[Skalarpotential]] oder einfach kurz das Potential des Gradientenfelds <math>\vec F</math>. | |||
Der Begriff Potential darf nicht mit dem ''physikalischen'' Begriff des „[[Potential (Physik)|Potential]]s“ verwechselt werden, mit dem die Fähigkeit eines [[Konservative Kraft|konservativen Kraftfelds]] bezeichnet wird, einen dem Feld ausgesetzten Körper eine Arbeit verrichten zu lassen. Physikalische Potentiale sind dabei stets auch Potentiale im Sinne der Mathematik, wenn damit die entsprechenden Ortsfunktionen (Felder) und nicht nur deren Funktionswerte gemeint sind. Jedoch ist umgekehrt nicht jedes mathematische Potential auch eines im oben genannten physikalischen Sinn, etwa das der [[potentielle Energie|potentiellen Energie]]<ref>W. Gellert, H. Küstner, M. Hellwich, H. Kästner: ''Kleine Enzyklopädie Mathematik.'' Leipzig 1970, S. 742.</ref> oder das [[Geschwindigkeitspotential]]. | |||
== Beispiele == | |||
[[Datei:Conservative fields.png|miniatur|hochkant=1.5|Beispiele von Potential- und Gradientenfeldern in der Physik<br /> | |||
''Skalarfelder (Potentialfelder) (<span style="background:yellow">gelb</span>)'':<br /> | |||
'''V<sub>G</sub>''' - [[Gravitationspotential]]<br /> | |||
'''W<sub>pot</sub>''' - [[potentielle Energie]]<br /> | |||
'''V<sub>C</sub>''' - [[Coulomb-Potential]]<br /> | |||
''Vektorfelder (Gradientenfelder) (<span style="background:cyan">cyan</span>)'':<br /> | |||
'''a<sub>G</sub>''' - [[Gravitationsbeschleunigung]]<br /> | |||
'''F''' - [[Kraft]]<br /> | |||
[[Datei:Conservative fields.png|miniatur|hochkant=1.5|Beispiele von Potential- und Gradientenfeldern in der Physik<br/> | |||
''Skalarfelder (Potentialfelder) (<span style="background:yellow">gelb</span>)'':<br/> | |||
'''V<sub>G</sub>''' - [[Gravitationspotential]]<br/> | |||
'''W<sub>pot</sub>''' - [[potentielle Energie]]<br/> | |||
'''V<sub>C</sub>''' - [[Coulomb-Potential]]<br/> | |||
''Vektorfelder (Gradientenfelder) (<span style="background:cyan">cyan</span>)'':<br/> | |||
'''a<sub>G</sub>''' - [[Gravitationsbeschleunigung]]<br/> | |||
'''F''' - [[Kraft]]<br/> | |||
'''E''' - [[elektrische Feldstärke]]]] | '''E''' - [[elektrische Feldstärke]]]] | ||
Leitet man das Feld der potentiellen Energie <math>W_\mathrm{pot}(\vec r)</math>, wie in der nebenstehenden Abb. gezeigt, nach dem Ort <math>\vec r</math> ab <ref name="Grimsehl 1" />, erhält man den Energie[[Gradient (Mathematik)|gradienten]] <math>\vec \nabla W_\mathrm{pot}(\vec r)</math>, also ein Vektorfeld, dessen einzelne Vektoren dabei in die Richtung der jeweils stärksten Zunahme von <math>W_\mathrm{pot}(\vec r)</math> an der Stelle <math>\vec r</math> zeigen. Dem [[Prinzip des kleinsten Zwanges]] folgend, sind die diesem Gradienten entgegengesetzten Vektoren <math>-\vec \nabla W_\mathrm{pot}(\vec r)</math> nichts anderes als die jeweils in Richtung des steilsten Gefälles von <math>W_\mathrm{pot}(\vec r)</math> zeigenden „rücktreibenden“ Kräfte <math>F_G</math> ([[Gravitationskraft]]) und <math>F_C</math> ([[Coulombkraft]]) | Leitet man das Feld der potentiellen Energie <math>W_\mathrm{pot}(\vec r)</math>, wie in der nebenstehenden Abb. gezeigt, nach dem Ort <math>\vec r</math> ab<ref name="Grimsehl 1" />, erhält man den Energie[[Gradient (Mathematik)|gradienten]] <math>\vec \nabla W_\mathrm{pot}(\vec r)</math>, also ein Vektorfeld, dessen einzelne Vektoren dabei in die Richtung der jeweils stärksten Zunahme von <math>W_\mathrm{pot}(\vec r)</math> an der Stelle <math>\vec r</math> zeigen. Dem [[Prinzip des kleinsten Zwanges]] folgend, sind die diesem Gradienten entgegengesetzten Vektoren <math>-\vec \nabla W_\mathrm{pot}(\vec r)</math> nichts anderes als die jeweils in Richtung des steilsten Gefälles von <math>W_\mathrm{pot}(\vec r)</math> zeigenden „rücktreibenden“ Kräfte <math>F_G</math> ([[Gravitationskraft]]) und <math>F_C</math> ([[Coulombkraft]]) | ||
:<math>\vec F_G = -\vec \nabla W_\mathrm{pot}(\vec r) \quad \text {bzw.} \quad \vec F_C = -\vec \nabla W_\mathrm{pot}(\vec r) </math>. | :<math>\vec F_G = -\vec \nabla W_\mathrm{pot}(\vec r) \quad \text {bzw.} \quad \vec F_C = -\vec \nabla W_\mathrm{pot}(\vec r) </math>. | ||
| Zeile 43: | Zeile 39: | ||
heißen [[Gravitationsbeschleunigung]] bzw. [[elektrische Feldstärke]]. | heißen [[Gravitationsbeschleunigung]] bzw. [[elektrische Feldstärke]]. | ||
== Vorzeichen == | |||
Handelt es sich bei dem zugrundeliegenden [[Skalarpotential]] auch um ein Potential im physikalischen Sinne (s. o.), beschreibt es also ein tatsächliches physikalisches [[Potential (Physik)|Arbeitsvermögen]], wird das sich aus ihm ergebende Gradientenfeld, wie gerade begründet, stets mit einem (der Zunahme des Betrags von <math>\vec r</math> entgegengesetzten) negativem [[Vorzeichen (Zahl)|Vorzeichen]] geschrieben. Bei Skalarfeldern dagegen, die sich nur mathematisch wie Potentiale verhalten, etwa dem [[Potentialströmung# | Handelt es sich bei dem zugrundeliegenden [[Skalarpotential]] auch um ein Potential im physikalischen Sinne (s. o.), beschreibt es also ein tatsächliches physikalisches [[Potential (Physik)|Arbeitsvermögen]], wird das sich aus ihm ergebende Gradientenfeld, wie gerade begründet, stets mit einem (der Zunahme des Betrags von <math>\vec r</math> entgegengesetzten) negativem [[Vorzeichen (Zahl)|Vorzeichen]] geschrieben. Bei Skalarfeldern dagegen, die sich nur mathematisch wie Potentiale verhalten, etwa dem [[Potentialströmung#Potentialströmung eines inkompressiblen Fluids|Strömungs- oder Geschwindigkeitspotential]], das damit auch keine potentielle Energie repräsentiert, ist das Vorzeichen seines Gradienten undefiniert und wird für gewöhnlich positiv gewählt: | ||
:Kraft - Potentielle Energie: <math>\quad \vec F(\vec r) = -\vec \nabla W_\mathrm{pot}(\vec r)</math><br/> | :Kraft - Potentielle Energie: <math>\quad \vec F(\vec r) = -\vec \nabla W_\mathrm{pot}(\vec r)</math><br /> | ||
:Elektrische Feldstärke - Coulomb-Potential: <math>\vec E(\vec r) = -\vec \nabla V_{C}(\vec r)</math><br/> | :Elektrische Feldstärke - Coulomb-Potential: <math>\vec E(\vec r) = -\vec \nabla V_{C}(\vec r)</math><br /> | ||
:Gravitationsbeschleunigung - Gravitationspotential: <math>\vec a_G(\vec r) = -\vec \nabla V_{G}(\vec r)</math> | :Gravitationsbeschleunigung - Gravitationspotential: <math>\vec a_G(\vec r) = -\vec \nabla V_{G}(\vec r)</math> | ||
:''aber'' | :''aber'' | ||
| Zeile 55: | Zeile 51: | ||
== Integrabilitätsbedingung == | == Integrabilitätsbedingung == | ||
Ist <math>U \subseteq \mathbb{R}^n</math> eine offene und [[Zusammenhängender Raum#Einfach zusammenhängend|einfach zusammenhängende]] (zum Beispiel [[Sterngebiet|sternförmige]]) Menge und <math>\vec F\colon U \to \mathbb{R}^n</math> [[Differentialrechnung#Ableitung als eine Funktion|stetig differenzierbar]], so ist <math>\vec F</math> genau dann ein Gradientenfeld, wenn die ''Integrabilitätsbedingungen'' | Ist <math>U \subseteq \mathbb{R}^n</math> eine offene und [[Zusammenhängender Raum#Einfach zusammenhängend|einfach zusammenhängende]] (zum Beispiel [[Sterngebiet|sternförmige]]) Menge und <math>\vec F\colon U \to \mathbb{R}^n</math> [[Differentialrechnung#Ableitung als eine Funktion|stetig differenzierbar]], so ist <math>\vec F</math> genau dann ein Gradientenfeld, wenn die ''Integrabilitätsbedingungen'' | ||
:<math>\frac{\partial F_i}{\partial x_j} = \frac{\partial F_j}{\partial x_i}</math> für alle <math>i,j \in \{1, \dots, n \}</math> | :<math>\frac{\partial F_i}{\partial x_j} = \frac{\partial F_j}{\partial x_i}</math> für alle <math>i,j \in \{1, \dots, n \}</math> | ||
auf <math>U</math> erfüllt ist. Die Aussage erhält man als Spezialfall aus dem [[Poincaré-Lemma]]. | auf <math>U</math> erfüllt ist. Die Aussage erhält man als Spezialfall aus dem [[Poincaré-Lemma]]. | ||
Im Zwei- und Dreidimensionalen lauten die Integrabilitätsbedingungen: | Im Zwei- und Dreidimensionalen lauten die Integrabilitätsbedingungen: | ||
*Für <math>\mathbb{R}^2</math>: <math>\frac{\partial F_1}{\partial x_2} = \frac{\partial F_2}{\partial x_1}</math> | *Für <math>\mathbb{R}^2</math>: <math>\frac{\partial F_1}{\partial x_2} = \frac{\partial F_2}{\partial x_1}</math> | ||
*Für <math>\mathbb{R}^3</math>: <math>\frac{\partial F_1}{\partial x_2} = \frac{\partial F_2}{\partial x_1},\ \frac{\partial F_1}{\partial x_3} = \frac{\partial F_3}{\partial x_1} \text{ und } \frac{\partial F_2}{\partial x_3} = \frac{\partial F_3}{\partial x_2}</math> <ref>K. Königsberger: ''Analysis 2.'' 5. Auflage. Springer, 2004, ISBN 3-540-20389-3, [[Korollar]] S. 193.</ref> | *Für <math>\mathbb{R}^3</math>: <math>\frac{\partial F_1}{\partial x_2} = \frac{\partial F_2}{\partial x_1},\ \frac{\partial F_1}{\partial x_3} = \frac{\partial F_3}{\partial x_1} \text{ und } \frac{\partial F_2}{\partial x_3} = \frac{\partial F_3}{\partial x_2}</math> <ref>K. Königsberger: ''Analysis 2.'' 5. Auflage. Springer, 2004, ISBN 3-540-20389-3, [[Korollar]] S. 193.</ref> | ||
Auf Gebieten, die nicht einfach zusammenhängend sind, sind diese Integrabilitätsbedingungen zwar [[ | Äquivalent dazu ist in beiden Fällen die Bedingung der Wirbelfreiheit <math>\operatorname{rot}\,\vec F= \vec 0</math>, also dass die [[Rotation eines Vektorfeldes|Rotation]] verschwindet. | ||
Auf Gebieten, die nicht einfach zusammenhängend sind, sind diese Integrabilitätsbedingungen zwar [[notwendige und hinreichende Bedingung|notwendig]], aber im Allgemeinen nicht [[notwendige und hinreichende Bedingung|hinreichend]]. | |||
== Wirbelfreiheit == | |||
Wie aus der Integrabilitätsbedingung folgt, sind Gradientenfelder rotations- bzw. wirbelfrei<ref name="KEM 547" /> | |||
:<math>\operatorname {rot}\,(\operatorname{grad}\,\Phi(\vec r)) = \operatorname {rot}\,\vec F(\vec r) = \vec \nabla \times \vec F(\vec r) = \vec 0</math>. | |||
Wichtig zu beachten ist, dass die Umkehrung nicht immer gilt. Nicht alle wirbelfreien Felder sind Gradientenfelder, sondern nur diejenigen, deren [[Definitionsmenge|Definitionsbereich]] [[Zusammenhängender Raum#Globale Zusammenhangsbegriffe|einfach zusammenhängend]] ist. | |||
== Einzelnachweise == | == Einzelnachweise == | ||
| Zeile 71: | Zeile 74: | ||
[[Kategorie:Vektoranalysis]] | [[Kategorie:Vektoranalysis]] | ||
[[Kategorie:Feldtheorie]] | [[Kategorie:Feldtheorie]] | ||
Aktuelle Version vom 16. Januar 2022, 00:21 Uhr
Ein Gradientenfeld oder konservatives Feld ist ein Vektorfeld, das aus einem Skalarfeld durch Differentiation nach dem Ort abgeleitet wurde, bzw. – kürzer formuliert – der Gradient des Skalarfelds. Dieses Vektorfeld hat die Eigenschaft, dass sein Kurvenintegral wegunabhängig ist.
Zur besseren Abgrenzung zwischen dem Gradienten als mathematischem Operator und dem Resultat seiner Anwendung bezeichnen manche Autoren die Vektoren, aus denen sich Gradientenfelder zusammensetzen, auch als Gradientvektoren,[1] andere dagegen mit Blick auf die Potentiale, aus denen sie sich herleiten, als Potentialvektoren[2].
Analog verwendet die überwiegende Zahl der Autoren den Begriff Potentialfeld nicht für das skalare Feld des Potentials selbst, sondern das sich aus ihm ableitende Gradientenfeld[3][4].
Definition
Es gibt mehrere äquivalente Definitionen:
- Ein Vektorfeld $ {\vec {F}}\colon {\vec {r}}\mapsto {\vec {F}}({\vec {r}}) $ heißt Gradientenfeld, wenn es ein Skalarfeld $ \Phi \colon {\vec {r}}\mapsto \Phi ({\vec {r}}) $ gibt, sodass gilt:
- $ {\vec {F}}({\vec {r}})={\vec {\nabla }}\Phi ({\vec {r}}) $
- Das Kurvenintegral ist wegunabhängig: Der Wert des Kurvenintegrals entlang einer beliebigen Kurve $ S $ innerhalb des Feldes ist nur von ihrem Anfangs- und Endpunkt abhängig, nicht dagegen von ihrer Länge.
- Kurvenintegrale über eine beliebige geschlossene Randkurve $ S $ ergeben immer Null:
- $ \oint _{S}{\vec {F}}({\vec {r}})\,\mathrm {d} {\vec {r}}=0 $
Hier wird mit $ {\vec {\nabla }} $ der Gradient bezeichnet. $ \Phi $ nennt man das zu $ {\vec {F}} $ gehörige Skalarpotential oder einfach kurz das Potential des Gradientenfelds $ {\vec {F}} $.
Der Begriff Potential darf nicht mit dem physikalischen Begriff des „Potentials“ verwechselt werden, mit dem die Fähigkeit eines konservativen Kraftfelds bezeichnet wird, einen dem Feld ausgesetzten Körper eine Arbeit verrichten zu lassen. Physikalische Potentiale sind dabei stets auch Potentiale im Sinne der Mathematik, wenn damit die entsprechenden Ortsfunktionen (Felder) und nicht nur deren Funktionswerte gemeint sind. Jedoch ist umgekehrt nicht jedes mathematische Potential auch eines im oben genannten physikalischen Sinn, etwa das der potentiellen Energie[5] oder das Geschwindigkeitspotential.
Beispiele
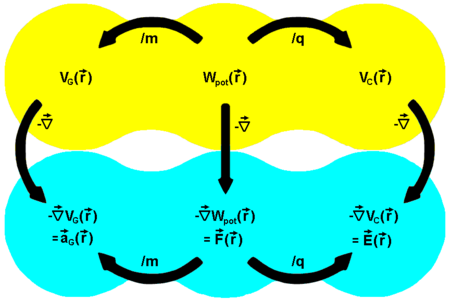
Skalarfelder (Potentialfelder) (gelb):
VG - Gravitationspotential
Wpot - potentielle Energie
VC - Coulomb-Potential
Vektorfelder (Gradientenfelder) (cyan):
aG - Gravitationsbeschleunigung
F - Kraft
E - elektrische Feldstärke
Leitet man das Feld der potentiellen Energie $ W_{\mathrm {pot} }({\vec {r}}) $, wie in der nebenstehenden Abb. gezeigt, nach dem Ort $ {\vec {r}} $ ab[1], erhält man den Energiegradienten $ {\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}}) $, also ein Vektorfeld, dessen einzelne Vektoren dabei in die Richtung der jeweils stärksten Zunahme von $ W_{\mathrm {pot} }({\vec {r}}) $ an der Stelle $ {\vec {r}} $ zeigen. Dem Prinzip des kleinsten Zwanges folgend, sind die diesem Gradienten entgegengesetzten Vektoren $ -{\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}}) $ nichts anderes als die jeweils in Richtung des steilsten Gefälles von $ W_{\mathrm {pot} }({\vec {r}}) $ zeigenden „rücktreibenden“ Kräfte $ F_{G} $ (Gravitationskraft) und $ F_{C} $ (Coulombkraft)
- $ {\vec {F}}_{G}=-{\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})\quad {\text{bzw.}}\quad {\vec {F}}_{C}=-{\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}}) $.
Division des Energiegradienten $ {\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}}) $ durch die Skalare m bzw. q liefert analog die Potentialgradienten $ {\vec {\nabla }}V_{G}({\vec {r}}) $ (Gravitationspotential) und $ {\vec {\nabla }}V_{C}({\vec {r}}) $ (Coulomb-Potential), deren einzelne Vektoren dabei abermals in Richtung der jeweils stärksten Zunahme des Potentials an der Stelle $ {\vec {r}} $ zeigen. Die ihnen entgegengesetzten Vektoren $ a_{G} $ und $ E $
- $ {\vec {a}}_{G}=-{\vec {\nabla }}V_{G}({\vec {r}})\quad {\text{bzw.}}\quad {\vec {E}}=-{\vec {\nabla }}V_{C}({\vec {r}}) $
heißen Gravitationsbeschleunigung bzw. elektrische Feldstärke.
Vorzeichen
Handelt es sich bei dem zugrundeliegenden Skalarpotential auch um ein Potential im physikalischen Sinne (s. o.), beschreibt es also ein tatsächliches physikalisches Arbeitsvermögen, wird das sich aus ihm ergebende Gradientenfeld, wie gerade begründet, stets mit einem (der Zunahme des Betrags von $ {\vec {r}} $ entgegengesetzten) negativem Vorzeichen geschrieben. Bei Skalarfeldern dagegen, die sich nur mathematisch wie Potentiale verhalten, etwa dem Strömungs- oder Geschwindigkeitspotential, das damit auch keine potentielle Energie repräsentiert, ist das Vorzeichen seines Gradienten undefiniert und wird für gewöhnlich positiv gewählt:
- Kraft - Potentielle Energie: $ \quad {\vec {F}}({\vec {r}})=-{\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}}) $
- Elektrische Feldstärke - Coulomb-Potential: $ {\vec {E}}({\vec {r}})=-{\vec {\nabla }}V_{C}({\vec {r}}) $
- Gravitationsbeschleunigung - Gravitationspotential: $ {\vec {a}}_{G}({\vec {r}})=-{\vec {\nabla }}V_{G}({\vec {r}}) $
- aber
- Geschwindigkeit - Geschwindigkeitspotential: $ {\vec {v}}({\vec {r}})=+{\vec {\nabla }}\Phi ({\vec {r}}) $
Integrabilitätsbedingung
Ist $ U\subseteq \mathbb {R} ^{n} $ eine offene und einfach zusammenhängende (zum Beispiel sternförmige) Menge und $ {\vec {F}}\colon U\to \mathbb {R} ^{n} $ stetig differenzierbar, so ist $ {\vec {F}} $ genau dann ein Gradientenfeld, wenn die Integrabilitätsbedingungen
- $ {\frac {\partial F_{i}}{\partial x_{j}}}={\frac {\partial F_{j}}{\partial x_{i}}} $ für alle $ i,j\in \{1,\dots ,n\} $
auf $ U $ erfüllt ist. Die Aussage erhält man als Spezialfall aus dem Poincaré-Lemma.
Im Zwei- und Dreidimensionalen lauten die Integrabilitätsbedingungen:
- Für $ \mathbb {R} ^{2} $: $ {\frac {\partial F_{1}}{\partial x_{2}}}={\frac {\partial F_{2}}{\partial x_{1}}} $
- Für $ \mathbb {R} ^{3} $: $ {\frac {\partial F_{1}}{\partial x_{2}}}={\frac {\partial F_{2}}{\partial x_{1}}},\ {\frac {\partial F_{1}}{\partial x_{3}}}={\frac {\partial F_{3}}{\partial x_{1}}}{\text{ und }}{\frac {\partial F_{2}}{\partial x_{3}}}={\frac {\partial F_{3}}{\partial x_{2}}} $ [6]
Äquivalent dazu ist in beiden Fällen die Bedingung der Wirbelfreiheit $ \operatorname {rot} \,{\vec {F}}={\vec {0}} $, also dass die Rotation verschwindet.
Auf Gebieten, die nicht einfach zusammenhängend sind, sind diese Integrabilitätsbedingungen zwar notwendig, aber im Allgemeinen nicht hinreichend.
Wirbelfreiheit
Wie aus der Integrabilitätsbedingung folgt, sind Gradientenfelder rotations- bzw. wirbelfrei[2]
- $ \operatorname {rot} \,(\operatorname {grad} \,\Phi ({\vec {r}}))=\operatorname {rot} \,{\vec {F}}({\vec {r}})={\vec {\nabla }}\times {\vec {F}}({\vec {r}})={\vec {0}} $.
Wichtig zu beachten ist, dass die Umkehrung nicht immer gilt. Nicht alle wirbelfreien Felder sind Gradientenfelder, sondern nur diejenigen, deren Definitionsbereich einfach zusammenhängend ist.
Einzelnachweise
- ↑ 1,0 1,1 Grimsehl: Lehrbuch der Physik, Bd. I. Leipzig 1954, S. 579.
- ↑ 2,0 2,1 W. Gellert, H. Küstner, M. Hellwich, H. Kästner: Kleine Enzyklopädie Mathematik. Leipzig 1970, S. 547.
- ↑ §4 Potentialfelder. (PDF; 1,8 MB) In: Mathematik für Ingenieure III. WS 2009/2010, Universität Kiel.
- ↑ Albert Fetzer, Heiner Fränkel: Mathematik 2: Lehrbuch für ingenieurwissenschaftliche Studiengänge. Springer, Berlin/Heidelberg, S. 322.
- ↑ W. Gellert, H. Küstner, M. Hellwich, H. Kästner: Kleine Enzyklopädie Mathematik. Leipzig 1970, S. 742.
- ↑ K. Königsberger: Analysis 2. 5. Auflage. Springer, 2004, ISBN 3-540-20389-3, Korollar S. 193.