Fluoreszenzkorrelationsspektroskopie
Die Fluoreszenzkorrelationsspektroskopie (englisch fluorescence correlation spectroscopy, FCS) ist eine höchstempfindliche optische Messmethode, die aus Fluktuationen in der Fluoreszenzintensität Informationen gewinnt. Mit FCS werden in der Regel Diffusionskonstanten, Konzentrationen und Bindungen zwischen verschiedenen diffundierenden Spezies gemessen. Die Methode wurde in den 1970er Jahren von Douglas Magde, Elliot Elson und Watt W. Webb entwickelt.[1]
Aufbau
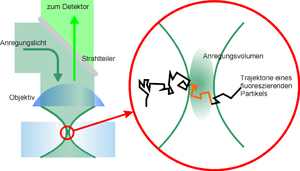
Die Grundlage für FCS bildet meist ein konfokales Mikroskop (siehe Abbildung). Das Anregungslicht wird mit Hilfe eines Objektives in die Probe fokussiert, so dass ein möglichst kleines Anregungsvolumen entsteht. Diffundieren nun fluoreszierende Teilchen (z. B. fluoreszenzmarkierte Proteine) in das Anregungsvolumen, so werden diese dort zur Fluoreszenz angeregt. Dabei absorbieren diese Teilchen die Photonen des Anregungslichtes und emittieren ihrerseits Photonen größerer Wellenlänge, also geringerer Energie. Die emittierten Photonen können jetzt den (für das Anregungslicht undurchlässigen) Strahlteiler passieren und werden dann mit einem Photodetektor detektiert. Wichtig ist dabei, dass die Ausleserate des Detektors um einige Größenordnungen über der typischen Aufenthaltszeit eines Teilchens im Fokus liegt. Für FCS werden heute hauptsächlich Avalanche-Photodioden eingesetzt, die einzelne Photonen detektieren können (SPAD). Es gibt aber auch Varianten, die z. B. auf EMCCD-Kameras basieren. In Verbindung mit Kameras kommen häufig auch andere Beleuchtungsmodalitäten zum Einsatz, wie etwa Interne Totalreflexionsfluoreszenzmikroskopie (TIR-FCS)[2] oder auch Lichtscheibenmikroskopie (SPIM-FCS),[3][4] die auch eine ortsaufgelöste Messung von Mobilitäten erlauben.
(Auto-)Korrelationsfunktion
Die eigentliche Messgröße bei der FCS ist die Fluoreszenzintensität als Funktion der Zeit $ F(t) $, meist Zeitspur genannt. Die Abbildung (oben) zeigt die Zeitspur einer stark verdünnten Probe. Jede Spitze in der Zeitspur steht für ein fluoreszierendes Teilchen, das gerade durch das Anregungsvolumen diffundiert. Jedes dieser Teilchen braucht eine bestimmte Zeit, um den Fokus zu durchqueren. Deshalb ist die Wahrscheinlichkeit groß, dass zu aufeinanderfolgenden Abtastzeiten von ein und demselben Teilchen Photonen detektiert werden. Man spricht davon, dass die gemessenen Intensitäten zeitlich korreliert sind. Um die Zeitspuren auszuwerten, werden sie mit sich selbst korreliert (autokorreliert). Die Autokorrelationsfunktion $ G(\tau ) $ ist wie folgt definiert:
- $ G(\tau ):={\frac {\langle \delta F(t)\delta F(t+\tau )\rangle }{\langle F(t)\rangle ^{2}}}={\frac {\langle F(t)F(t+\tau )\rangle }{\langle F(t)\rangle ^{2}}}-1 $.
Die spitzen Klammern bedeuten eine Mittlung über die Zeit, und $ \delta F(t)=F(t)-\langle F(t)\rangle $.
Die Abbildung (unten) zeigt die Autokorrelation der Fluoreszenzzeitspur, wobei man die logarithmische Skala der Zeitachse beachten muss. Der Abfall der Autokorrelationsfunktion auf ihren halben Startwert ist ein Maß für die Diffusionszeit $ \tau _{D} $. Diese gibt an, wie lange ein Teilchen im Durchschnitt braucht, um das Anregungsvolumen zu durchqueren. Für die freie dreidimensionale Diffusion lässt sich zeigen, dass die Autokorrelationsfunktion wie folgt ausgedrückt werden kann:
- $ G(\tau )={\frac {1}{\langle N\rangle }}{\frac {1}{1+{\frac {\tau }{\tau _{D}}}}}{\frac {1}{\sqrt {1+{\frac {\omega ^{2}}{z^{2}}}\cdot {\frac {\tau }{\tau _{D}}}}}} $
$ \langle N\rangle $ ist die mittlere Teilchenzahl im Anregungsvolumen (Fokus), $ \omega $ der laterale Fokusdurchmesser und $ z $ der axiale Fokusdurchmesser. Die Intensitätsverteilung des Anregungslichtes wird hier als dreidimensionale Gauß-Funktion angenommen, was für viele Mikroskopobjektive eine gute Näherung darstellt.
Aus $ \langle N\rangle $ lässt sich die Konzentration $ C $ der fluoreszenzaktiven Teilchen in der Lösung angeben, wenn man das Anregungsvolumen $ V $ kennt: $ \langle C\rangle ={\frac {\langle N\rangle }{V}} $. Die Diffusionskonstante ergibt sich aus $ D={\frac {\omega ^{2}}{4\tau _{D}}} $.
Für zweidimensionale Diffusion (z. B. in Zellmembranen) entfällt der Wurzelterm.
Anwendungen
- In der molekularen Biophysik kann man über die Abhängigkeit des Diffusionskoeffizienten vom hydrodynamischen Radius Rückschlüsse auf die Größe eines Proteins und damit, vor allem in Kombination mit dem Förster-Resonanzenergietransfer (FRET), seines Faltungszustands ziehen.
- Im Forschungsbereich der Zellbiologie gibt es vermehrt Arbeitsgruppen, die FCS in lebenden Zellen durchführen. Mittlerweile ist es möglich, mit entsprechend ausgestatteten kommerziellen konfokalen Mikroskopen Fluoreszenz-Korrelationsmessungen durchzuführen, wobei auch FCS-Erweiterungen für bestehende ältere Systeme angeboten werden.
- Im Bereich der Biotechnologie werden u. a. Screening-Roboter angeboten, die auf Autokorrelationsmessungen basieren.
Siehe auch
- Fluoreszenz-Lebenszeit-Korrelations-Spektroskopie (engl. {{Modul:Vorlage:lang}} Modul:Multilingual:149: attempt to index field 'data' (a nil value), FLCS)
Literatur
- Douglas Magde, Elliot Elson, W. W. Webb: Thermodynamic Fluctuations in a Reacting System—Measurement by Fluorescence Correlation Spectroscopy. In: Physical Review Letters. Band 29, Nr. 11, 1972, S. 705–708, doi:10.1103/PhysRevLett.29.705.
- Elliot L. Elson, Douglas Magde: Fluorescence correlation spectroscopy. I. Conceptual basis and theory. In: Biopolymers. Band 13, Nr. 1, 1974, S. 1–27, doi:10.1002/bip.1974.360130102.
- Douglas Magde, Elliot L. Elson, Watt W. Webb: Fluorescence correlation spectroscopy. II. An experimental realization. In: Biopolymers. Band 13, Nr. 1, 1974, S. 29–61, doi:10.1002/bip.1974.360130103.
- M. Ehrenberg, R. Rigler: Rotational brownian motion and fluorescence intensify fluctuations. In: Chemical Physics. Band 4, Nr. 3, 1974, S. 390–401, doi:10.1016/0301-0104(74)85005-6.
- R. Rigler, E. Elson: Fluorescence correlation spectroscopy: theory and applications. Springer, 2001, ISBN 3-540-67433-0.
- P. Schwille, E. Haustein: Fluorescence correlation spectroscopy. An introduction to its concepts and applications. In: Biophysics Textbook Online. Band 1, Nr. 3, 2001 (biophysics.org [PDF; 1,1 MB]).
Einzelnachweise
- ↑ Douglas Magde, Elliot Elson, W. W. Webb: Thermodynamic Fluctuations in a Reacting System—Measurement by Fluorescence Correlation Spectroscopy. In: Physical Review Letters. Band 29, Nr. 11, 1972, S. 705–708, doi:10.1103/PhysRevLett.29.705.
- ↑ Balakrishnan Kannan, Lin Guo, Thankiah Sudhaharan, Sohail Ahmed, Ichiro Maruyama, Thorsten Wohland: Spatially Resolved Total Internal Reflection Fluorescence Correlation Microscopy Using an Electron Multiplying Charge-Coupled Device Camera. In Analytical Chemistry. 79, 2007, S. 4463–4470, doi:10.1021/ac0624546
- ↑ T. Wohland, X. Shi, J. Sankaran, E. H. Stelzer: Single plane illumination fluorescence correlation spectroscopy (SPIM-FCS) probes inhomogeneous three-dimensional environments. In Optics express, Band 18, Nr. 10, 2010, ISSN 1094-4087, S. 10627–10641, PMID 20588915
- ↑ J. Capoulade, M. Wachsmuth, L. Hufnagel, M. Knop: Quantitative fluorescence imaging of protein diffusion and interaction in living cells. In Nature Biotechnology. Band 29, Nr. 9, 2011, ISSN 1087-0156, S. 835–839. doi:10.1038/nbt.1928, PMID 21822256