Korrelationsungleichung

Als Korrelationsungleichungen werden eine Gruppe von mathematischen Ungleichungen bezeichnet, welche den Begriff der positiven Korrelation auf partiell geordnete Mengen (POSETs) und distributive Verbände übertragen. Sie haben darüber hinaus eine wahrscheinlichkeitstheoretische Interpretation und berühren das mathematische Teilgebiet der Theorie der stochastischen Ordnungen.

Die Entwicklung wurde angestoßen durch die FKG-Ungleichung aus dem Jahr 1971, benannt nach C. M. Fortuin, Jean Ginibre und P. W. Kasteleyn, welche auf verschiedensten Gebieten Anwendung gefunden hat, unter anderem auf den Gebieten statistische Mechanik, Partikelsysteme, Kombinatorik und Perkolationstheorie.^[1] Eine frühere Version dieser Ungleichung für unabhängige und identisch verteilte Zufallsvariablen wurde 1960 von Theodore Edward Harris bewiesen^[2], wurde jedoch zunächst nicht von Mathematikern anderer Disziplinen rezipiert^[3] und erst durch die Veröffentlichung von Fortuin, Kasteleyn und Ginibre bekannt. In diesem Zusammenhang spielt der Begriff des assoziierten Maßes (auch Maß mit positiven Korrelationen) eine Rolle.

Ausgehend von der FKG-Ungleichungen wurden weitere ähnliche Ungleichungen gefunden, zum Beispiel die Holley-Ungleichung nach Richard Holley im Jahr 1974, oder die sehr allgemeine Vier-Funktionen-Ungleichung von Rudolf Ahlswede und David E. Daykin von 1978, aus der die anderen genannten Ungleichungen folgen.

Assoziierte Maße

Der Begriff des assoziierten Maßes wurde 1967 von J. D. Esary, Frank Proschan und D. W. Walkup^[4] eingeführt. Wegen der Analogie zu positiven Korrelationen von Zufallsvariablen wird von manchen Autoren auch die Bezeichnung Maß mit positiven Korrelationen verwendet.

Ein endliches Maß $ \mu $ auf $ (X,{\mathfrak {B}}) $, wobei $ X $ ein halbgeordneter topologischer^[5] Raum sei, heißt assoziiert, falls

$ \int fg\;\mathrm {d} \mu \geq \int f\mathrm {d} \mu \cdot \int g\mathrm {d} \mu $

für alle beschränkten, stetigen, monoton wachsenden Funktionen $ f,g $ von $ X $ nach $ \mathbb {R} $ gilt.

Die FKG-Ungleichung

Die FKG-Ungleichung, benannt nach C. M. Fortuin, J. Ginibre und P. W. Kasteleyn (1971), ist ursprünglich eine Korrelationsungleichung auf distributiven Verbänden. Sie ist ein fundamentales Werkzeug auf den Gebieten der statistischen Mechanik und der probabilistischen Kombinatorik (speziell auf dem Gebiet der Zufallsgraphen.) Sie besagt übertragen auf ein wahrscheinlichkeitstheoretisches Setting in etwa, dass wachsende Ereignisse miteinander positiv korreliert sind.

Formulierung für endliche distributive Verbände

Sei $ X $ ein endlicher distributiver Verband, und $ \mu $ ein Maß auf $ X $, welches

$ \mu (\{x\wedge y\})\mu (\{x\vee y\})\geq \mu (\{x\})\mu (\{y\}) $

für alle $ x $, $ y $ im Verband $ X $ erfüllt. Diese Eigenschaft heißt auch Log-Supermodularität.

Die FKG-Ungleichung besagt dann, dass das Maß $ \mu $ assoziiert ist, also dass für zwei beliebige bezüglich der von den Verbandsoperationen induzierten Halbordnung stetige, monoton wachsende, quadratintegrierbare Funktionen $ f $ und $ g $ von $ X $ nach $ \mathbb {R} $ gilt, dass sie positiv korreliert sind:

$ \int fg\;\mathrm {d} \mu \geq \int f\mathrm {d} \mu \cdot \int g\mathrm {d} \mu $.

Ebenfalls positiv korreliert sind zwei Funktionen $ f $ und $ g $, wenn man die Bedingung „monoton steigend“ durch „monoton fallend“ ersetzt. Ist die eine Funktion monoton wachsend, die andere monoton fallend, dann sind sie negativ korreliert. Ein Beweis befindet sich in der Originalarbeit.

Eine ähnliche Aussage gilt im allgemeineren Fall, dass $ X $ ein abzählbarer kompakter metrischer Raum ist. In diesem Fall muss $ \mu $ ein strikt positives endliches Maß sein und die Log-Supermodularität muss über Randereignisse (Zylindermengen) definiert werden.^[6]

Weitere Formulierungen

In Rinott, Saks findet sich der Beweis für eine Form der FKG-Ungleichung für $ \sigma $-finite Maße auf der (überabzählbaren) Menge $ \mathbb {R} ^{d} $. In diesem Fall wird Log-Supermodularität eines Maßes über die Dichtefunktion $ \varphi $ (bezüglich irgendeines Produktmaßes auf $ \mathbb {R} ^{d} $) definiert, welche für alle $ x,y\in \mathbb {R} ^{d} $ erfüllen muss:

$ \varphi (x)\varphi (y)\leq \varphi (x\wedge y)\varphi (x\vee y) $.

Die Griffith-Ungleichung ist eine weitere Ungleichung von 1967, welche die gleiche Aussage macht wie die FKG-Ungleichung, jedoch andere Voraussetzungen hat und Anwendung auf dem Gebiet des Ising-Modells hat.^[7]

Die Harris-Ungleichung

Die Harris-Ungleichung ist im Prinzip die FKG-Ungleichung für Produktmaße, benannt nach Theodore E. Harris, welcher sie 1960 beim Studium von Perkolationen in der Ebene gefunden hat.^[8]

Wenn $ X $ eine totalgeordnete Menge ist, dann ist die Log-Supermodularität automatisch für jedes Maß $ \mu $ auf $ X $ erfüllt.

Es gilt zum Beispiel, dass für jede Wahrscheinlichkeitsverteilung $ \mu $ auf $ \mathbb {R} $, und monoton wachsende quadratintegrierbaren Funktionen $ f $ und $ g $

$ \int _{\mathbb {R} }f(x)g(x)\,d\mu (x)\geq \int _{\mathbb {R} }f(x)\,d\mu (x)\,\int _{\mathbb {R} }g(x)\,d\mu (x), $

gilt. Dies folgt aus

$ \int _{\mathbb {R} }\int _{\mathbb {R} }[f(x)-f(y)][g(x)-g(y)]\,d\mu (x)\,d\mu (y)\geq 0 $

(die Terme in den eckigen Klammern haben das jeweils gleiche Vorzeichen.)

Die Log-Supermodularität ist auch automatisch erfüllt, wenn der Verband ein Produkt totalgeordneter Verbände ist, $ X=X_{1}\times \dots \times X_{n} $, und $ \mu =\mu _{1}\otimes \dots \otimes \mu _{n} $ ein Produktmaß auf $ X $. In der Anwendung ist $ \mu $ häufig die (Produkt-)Verteilung von unabhängig und identisch verteilten Zufallsvariablen auf unabhängigen Kopien $ X_{i} $ eines Wahrscheinlichkeitsraumes.

Sei $ E $ eine endliche Indexmenge. Sei $ X=\prod _{e\in E}\{0,1\} $ versehen mit der koordinatenweisen Ordnung $ \leq $ und mit den Verbands-Operationen:

$ \xi \vee \eta $ sei für alle $ \xi ,\eta \in X $, $ e\in E $ definiert über $ \xi (e)\vee \eta (e):=\max\{\xi (e),\eta (e)\} $,

sowie $ \xi \wedge \eta $ entsprechend über $ \xi (e)\wedge \eta (e):=\min\{\xi (e),\eta (e)\} $.

Mit diesen Operationen ist $ X $ eine Boolesche Algebra.

Sei $ \mu $ ein Wahrscheinlichkeitsmaß auf $ (X,\wp (X)) $. Dann schreibt sich die FKG-Ungleichung

$ \mathbf {E} _{\mu }fg\geq (\mathbf {E} _{\mu }f)(\mathbf {E} _{\mu }g) $

für alle monoton wachsenden $ f,g $ für die die Erwartungswerte existieren, wobei $ \mathbf {E} _{\mu } $ den Erwartungswert bezüglich $ \mu $ bezeichne.^[9]

Ein Ereignis $ A\in \wp (X) $ heißt entsprechend wachsend, wenn $ \mathbb {I} _{A}(x)\leq \mathbb {I} _{A}(y) $ für alle $ x,y\in X $ mit $ x\leq y $. (Und ein Ereignis heißt fallend, wenn das Komplement $ \Omega \setminus A $ wachsend ist.)

Sind $ A $ und $ B $ wachsende Ereignisse, so gilt

$ \mathbf {P} _{\mu }(A\cap B)\geq \mathbf {P} _{\mu }(A)\mathbf {P} _{\mu }(B). $

Ein Beweis der Harris-Ungleichung, der auf dem hier verwendeten Doppelintegral-Trick auf $ \{0,1\} $ beruht, findet sich in Grimmett 1999.

Beispiele

Honigwabengitter mit zufällig eingefärbten Waben.

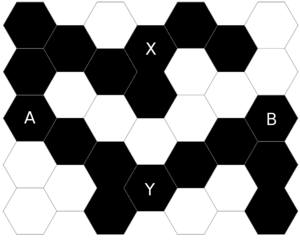
Man färbe zufällig jedes Hexagon des unendlichen Honigwaben-Gitters schwarz jeweils stochastisch unabhängig voneinander mit Wahrscheinlichkeit $ p $ und weiß mit Wahrscheinlichkeit $ 1-p $. Seien $ A,B,X,Y $ vier (nicht notwendig verschiedene) solche Hexagone. Seien $ A\leftrightarrow B $ und $ X\leftrightarrow Y $ die Ereignisse, dass es einen schwarzen Pfad von $ A $ nach $ B $ respektive von $ X $ nach $ Y $gibt. Dann besagt die FKG-Ungleichung, dass diese Ereignisse positive korreliert sind: $ \mathbf {P} (A\leftrightarrow B,\ X\leftrightarrow Y)\geq \mathbf {P} (A\leftrightarrow B)\mathbf {P} (X\leftrightarrow Y) $. In anderen Worten, wird vorausgesetzt, dass es bereits den einen schwarzen Pfad gibt, wird die Existenz des anderen Pfades wahrscheinlicher.

Im Erdős-Rényi-Zufallsgraph ist die Existenz eines Hamilton-Zyklus negativ korreliert mit der 3-Färbbarkeit des Graphen, da die Wahrscheinlichkeit der Existenz eines Hamilton-Zyklus mit der Anzahl der belegten Verbindungen steigt (steigendes Ereignis), während die Wahrscheinlichkeit von letzterem fällt (fallendes Ereignis).

Die Holley-Ungleichung

Diese von Richard Holley 1974 entdeckte und gelegentlich als Holley-Ungleichung bezeichnete Ungleichung besagt: Seien $ \mu _{1} $ und $ \mu _{2} $ zwei strikt positive Verteilungen auf einem endlichen distributiven Verband $ X $, welche

$ \mu _{1}(\{x\wedge y\})\mu _{2}(\{x\vee y\})\geq \mu _{1}(\{x\})\mu _{2}(y\}) $ für alle $ x,y\in X $

erfüllen. Dann gilt

$ \int f\;\mathrm {d} \mu _{2}\geq \int f\;\mathrm {d} \mu _{1} $.

für alle monoton wachsende integrierbaren Funktionen $ f $ auf $ X $. Dies ist gleichbedeutend damit, dass $ \mu _{2} $ größer als $ \mu _{1} $ bezüglich der gewöhnlichen stochastischen Ordnung ist. Thomas Liggett hat einen Beweis für Räume der Form $ \Omega =\prod _{s\in S}\{0,1\} $, welcher auf der Kopplung zweier Markow-Ketten in stetiger Zeit mit $ \mu _{1} $ und $ \mu _{2} $ als stationären Verteilungen beruht. Er gibt darüber hinaus an, wie der Beweis auf abzählbare Produkträume zu erweitern wäre.^[10] Aus der Holley-Ungleichung lässt sich die FKG-Ungleichung durch geschicktes Einsetzen folgern.^[11]

Alternative Voraussetzung für die FKG-Ungleichung

Sei $ \mathbb {R} ^{d} $ versehen mit der koordinatenweisen Halbordnung. Für eine Verteilung $ \mu $ auf $ \mathbb {R} ^{d} $ ist folgende Eigenschaft oft leichter zu überprüfen als die Log-Supermodularität:

Fixiert man eine Koordinate $ i\in \{1,\dots ,d\} $ und zwei Konfigurationen $ \varphi $ und $ \psi $ in $ \mathbb {R} ^{d} $ bezüglich der anderen Koordinaten, so dass $ \varphi _{j}\geq \psi _{j} $ for all $ w\not =v $, die auf $ \mu $ bedingte Verteilung von $ \varphi _{i} $ gegeben $ \{\varphi (j):j\not =i\} $ ist stochastisch größer als die auf $ \mu $ bedingte Verteilung von $ \psi $ gegeben $ \{\psi _{j}:j\not =i\} $.

Erfüllt $ \mu $ diese Eigenschaft, dann ist $ \mu $ assoziiert.

Die Vier-Funktionen-Ungleichung

Die Vier-Funktionen-Ungleichung von Ahlswede and Daykin von 1978 lässt sich wie folgt formulieren: Seien $ f_{1},f_{2},g_{1},g_{2} $ nichtnegative reellwertige Funktionen auf $ \mathbb {R} ^{d} $, welche folgende Bedingung erfüllen:

$ f_{1}(x)f_{2}(y)\leq g_{1}(x\vee y)g_{2}(x\wedge y) $ für alle $ x,y $

Dann gilt für jedes log-supermodulare Maß $ \mu $ auf $ \mathbb {R} ^{d} $,

$ \int _{\mathbb {R} ^{d}}f_{1}(x)\mathrm {d} \mu (x)\int _{\mathbb {R} ^{d}}f_{2}(x)\mathrm {d} \mu (x)\leq \int _{\mathbb {R} ^{d}}g_{1}(x)\mathrm {d} \mu (x)\int _{\mathbb {R} ^{d}}g_{2}(x)\mathrm {d} \mu (x) $

Es lässt sich zeigen, dass aus der Vier-Funktionen-Ungleichung Holleys Ungleichung folgt, aus der wiederum die FKG-Ungleichung folgt.^[12]

Einzelnachweise

Literatur

• C. M. Fortuin, P.W. Kasteleyn, J. Ginibre: Correlation inequalities on some partially ordered sets. In: Comm. Math. Phys. Nr. 22, 1971, MR0309498, ISSN 0010-3616, S. 89–103.
• P.C. Fishburn: FKG inequality. In: Michiel Hazewinkel (Hrsg.): Encyclopaedia of Mathematics, Kluwer Academic Publishers, 2001, ISBN 978-1-55608-010-4.
• P.C. Fishburn: Correlation inequalities. In: Michiel Hazewinkel (Hrsg.): Encyclopaedia of Mathematics, Kluwer Academic Publishers, 2001, ISBN 978-1-55608-010-4.
• H.-O. Georgii, O. Haggstrom, C. Maes: The random geometry of equilibrium phases. In: Phase transitions and critical phenomena. Nr. 18, 2001, Academic Press, San Diego, CA, MR2014387, S. 1–142.
• G. R. Grimmett: Percolation. Second edition. Springer-Verlag, New York 1999, MR1707339, ISBN 3-540-64902-6.
• T. E. Harris: A lower bound for the critical probability in a certain percolation. In: Proceedings of the Cambridge Philosophical Society, Nr. 56, 1960, MR0115221, S. 13–20.
• R. Holley: Remarks on the FKG inequalities. In: Communications in Mathematical Physics Nr. 36, 1974, MR0341552, ISSN 0010-3616, S. 227–231.
• Thomas M. Liggett: Interacting Particle Systems. Springer-Verlag, New York, 1985. ISBN 3-540-96069-4.
• R. Lyons: Phase transitions on nonamenable graphs In: J. Math. Phys. Nr. 41, 2000, MR1757952, S. 1099–1126.
• S. Sheffield: Random surfaces. In: Asterisque, Nr. 304, 2005, MR2251117.
• A. Müller and D. Stoyan: Comparison Methods for Stochastic Models and Risk. Wiley, Chichester, 2002.
• Yosef Rinott, Michael Saks: On FKG-type and permanental inequalities. In: Moshe Shaked, Y. L. Tong (Hrsg.): Stochastic inequalities: Papers from the AMS-IMS-SIAM Joint Summer Research Conference held in Seattle, Washington. July 1991 (Hayward, CA: Institute of Mathematical Statistics, 1992), ISBN 0-940600-29-3, ISBN 978-0-940600-29-4, 332–342, MR1228073.